Il y a risque d’épidémie dès qu’une maladie est suffisamment contagieuse pour qu’un individu malade ait le temps de contaminer plus d’un autre individu sur la période de sa maladie (voir ici. Cela déclenche une réaction en chaîne difficile à arrêter. L’objectif sanitaire des mesures qui sont prises est de limiter cette propagation exponentielle de la maladie en faisant baisser ce nombre moyen d’individus qu’un unique malade va contaminer. En lui-même, un virus est plus ou moins contagieux mais il y a deux dimensions à la contagiosité sur lesquelles nous pouvons agir :
-
La probabilité de transmission à chaque interaction : les gestes barrières sont là pour réduire cette probabilité de transmission : porter un masque, se tenir à plus d’un mètre, se laver les mains, éviter les poignées de mains etc.
-
Le nombre d’interactions : les mesures de distanciation physique comme le confinement limitent le nombre de contacts physiques ou de discussion prolongées et donc les occasions de transmission.
Dans cette question, nous allons nous intéresser principalement à cette seconde dimension.
Dès le début du confinement, les journaux télévisés traitaient ce sujet, mettant en avant que dans une journée typique, un parisien pouvait se retrouver dans une situation de grande proximité physique avec en moyenne 50 individus : travail, transports en commun, courses, loisirs… Des études, réalisées en Europe, aux États-Unis et en France montrent que, en moyenne chaque jour, un individu a des contacts (physiques ou discussions prolongées) avec 7 à 14 autres personnes (voir (1), (2), (3) et (4)).
Comme dans toute épidémie de ce type, on savait que pour limiter la propagation du virus de la COVID19, il fallait limiter le nombre d’interactions. Il ne s’agit pas ici de discuter cette proposition et ses conséquences sociales ou économiques mais de se poser la question de la forme de notre réseau interpersonnel. En effet lors du confinement chaque individu rencontre mécaniquement moins de monde mais l’ensemble des contacts persistants dessine toujours un réseau social particulier et la forme de ce nouveau réseau pourrait bien être plus ou moins efficace pour limiter la propagation du virus.
Il existe déjà une réponse intuitive à cette question dans les questions précédentes. Dans la question 5 sur le trafic aérien, on voit que la forme du réseau aérien n’est pas quelconque mais suit une logique, avec des aéroports principaux qui redistribuent le trafic vers des aéroports secondaires, et qu’en fonction du rôle plus ou moins central de l’aéroport et du lieu de départ de la maladie, elle va se propager à différents rythmes. Dans les modèles sur le confinement notamment aux questions 9 et 13, les rencontres des agents à l’extérieur et à l’intérieur de leur foyer dessinent un réseau d’interactions particulier. Dans ces modèles, le foyer semble devenir un accélérateur de la propagation de la maladie : le contact répété augmente le risque de transmission et les conjoints vont ensuite propager le virus sur leur lieu de travail par exemple.
Il est vain de vouloir explorer ici tous les réseaux sociaux possibles. En effet, la complexité mathématique est grande : pour 5 individus (par exemple), nous pourrions dessiner jusqu’à 1024 réseaux d’interactions différents les reliant : en partant de “personne n’est en lien avec personne”, jusqu’à “tout le monde est en lien avec tout le monde”. Si, si, c’est mathématique ! Heureusement, parmi ces 1024 possibilités beaucoup se ressemblent donc il n’y a pas besoin de tout essayer, on peut se contenter de ne s’intéresser qu’à certaines formes particulières qui ont déjà été étudiées par les sciences sociales et les mathématiques.
Nous allons reprendre certaines de ces formes et montrer leur influence potentiel sur la propagation d’un virus comme celui de la COVID 19.
Le modèle
Dans le modèle, il y a 200 agents et parmi ces agents, un seul est porteur de la maladie.
Les agents sont reliés par des liens (de couleur rose pâle) qui constituent leur réseau social. Nous choisissons un nombre moyen de liens de 10 par agent (entre les 7 et 14 contacts évoqués plus haut).
À chaque pas de temps, qui pourrait être caricaturalement vu comme une journée, un agent interagit avec tous les agents dans son réseau. Si un agent malade interagit avec un agent sain, ce dernier aura une certaine probabilité d’être infecté. S’il est infecté l’agent ainsi que le lien qui a permis l’interaction contaminante deviennent de couleur noire. Dans les illustrations qui suivront, nous fixerons généralement à 5% la probabilité de transmission de la maladie lors d’une interaction.
Nous considérerons qu’un agent malade n’est pas contagieux le jour même où il est infecté, mais dès le lendemain.
Il ne nous reste alors plus qu’à tester le modèle avec différentes formes de réseaux et voir comment se comporte la dynamique épidémique.
Pour représenter nos réseaux, nous faisons le choix ici de disposer les agents en cercle et en quinconce, cela aura son importance sur la lisibilité des résultats pour certains réseaux.
Les formes de réseaux
Réseau complet
Souvent, pour comprendre pas à pas les dynamiques dans les modèles, il est utile de partir de cas particuliers. Pour les réseaux, on part généralement du réseau complet où tout le monde est en interaction avec tout le monde et pas de surprise, la maladie se propage très rapidement.
Illustration : Avec une probabilité de transmission de 100%, l’agent “zéro” infecte tout le monde en un seul pas de temps.

Illustration : Avec une probabilité de transmission de 5%, il ne faut guère plus de 3 pas de temps avant que tout le monde soit infecté.

Réseau aléatoire
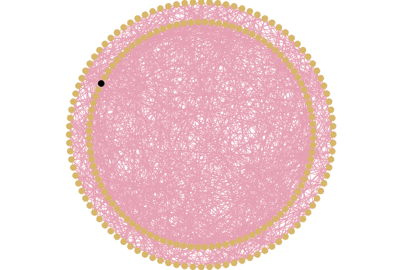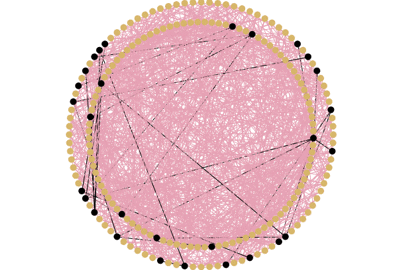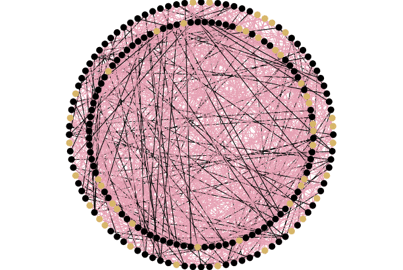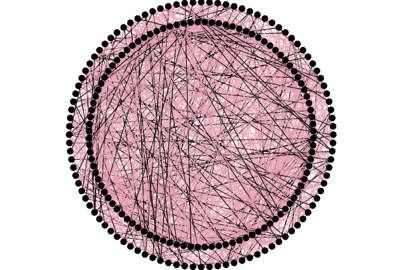
Ensuite, nous pouvons tester une autre forme classique de réseau dite “aléatoire”. Il suffit de définir le nombre moyen de liens par agent que l’on souhaite et de créer aléatoirement ces liens entre les agents. On observe que la maladie se propage bien sûr moins vite que dans un réseau complet et de manière assez erratique en raison du caractère aléatoire des liens.
Illustration : Réseau aléatoire avec 10 liens en moyenne par agent.
Réseau à forte densité locale
Contrairement à ce qui se passe dans un réseau aléatoire, une des caractéristiques principales des réseaux sociaux humains est le fait que souvent les amis de nos amis sont aussi nos amis. On parle de cliques. Le réseau suivant que nous appellerons réseau régulier à forte densité locale en est un très bon exemple.
Illustration : Avec 10 amis en moyenne par agent et une probabilité de transmission de la maladie de 5%. Les agents sont disposés en cercle et leurs amis sont uniquement les agents les plus proches d’eux dans le cercle. Dans cet exemple, les 10 amis d’un agent seront les 5 agents directement à sa droite et les 5 agents directement à sa gauche dans le cercle.


On remarque, avec le réseau régulier à forte densité locale une propagation plus lente et linéaire de la maladie. Elle se propage d’abord dans le groupe d’amis du premier agent infecté. Ensuite, elle se répand lentement autour du cercle de proche en proche à partir de ce groupe d’amis initial. Comparativement au réseau aléatoire, ce ralentissement de la propagation de la maladie est lié à la caractéristique d’entre-soi de ce réseau à densité locale forte qui fait que la maladie devient rapidement « prisonnière » des groupes d’amis : elle ne peut plus facilement se répandre car elle manque d’interactions avec de nouveaux agents sains à l’extérieur du groupe d’amis infecté.
Réseau de type “petit monde” (small world)
En plus, du fait que les amis de nos amis sont souvent aussi nos amis, les réseaux sociaux humains ont une seconde caractéristique importante qui est que nous ne sommes pas socialement très distants d’un inconnu. Nous avons tous déjà entendu dire, que nous ne sommes pas séparé d’un autre individu de la planète par plus de 5 autres individus (voir ici et (5)). Cela serait possible grâce à des “passerelles” entre les groupes d’amis. Par exemple, supposons que votre cousin et ses amis ne connaissent aucun de vos amis et que vous ne connaissiez aucun des amis de votre cousin. La relation que vous entretenez avec lui fait que ses amis et les vôtres ne sont finalement pas très distants socialement : deux individus seulement les séparent, vous et votre cousin même si votre cousin vit au Japon!
Les réseaux dits “small world” regroupent les deux caractéristiques importantes des réseaux sociaux humains que nous venons d’évoquer.
Illustration : Avec 10 amis en moyenne par agent et une probabilité de transmission de la maladie de 5%. Pour faire un “small world”, on part d’un réseau régulier à forte densité locale , qui assure le fait que les amis de vos amis ont de fortes chances d’être vos amis. Ensuite, un certain nombre de ces liens sont rompus et recréés aléatoirement avec d’autres agents n’importe où dans le cercle ce qui crée des raccourcis entre les groupes d’amis. Ce sont les “passerelles” que nous avons évoquée plus haut.
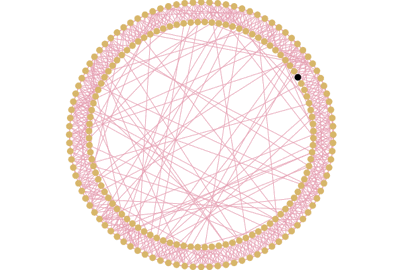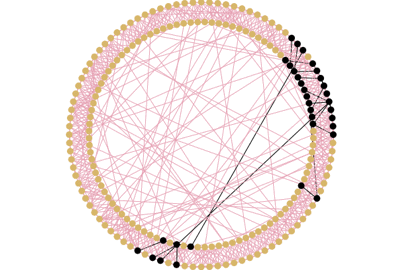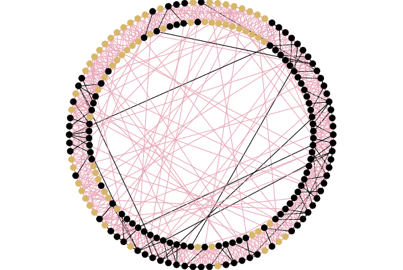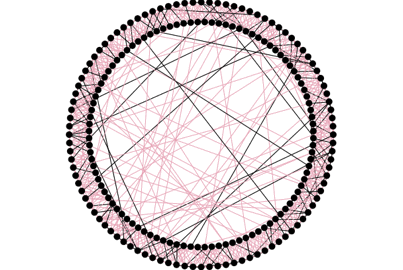
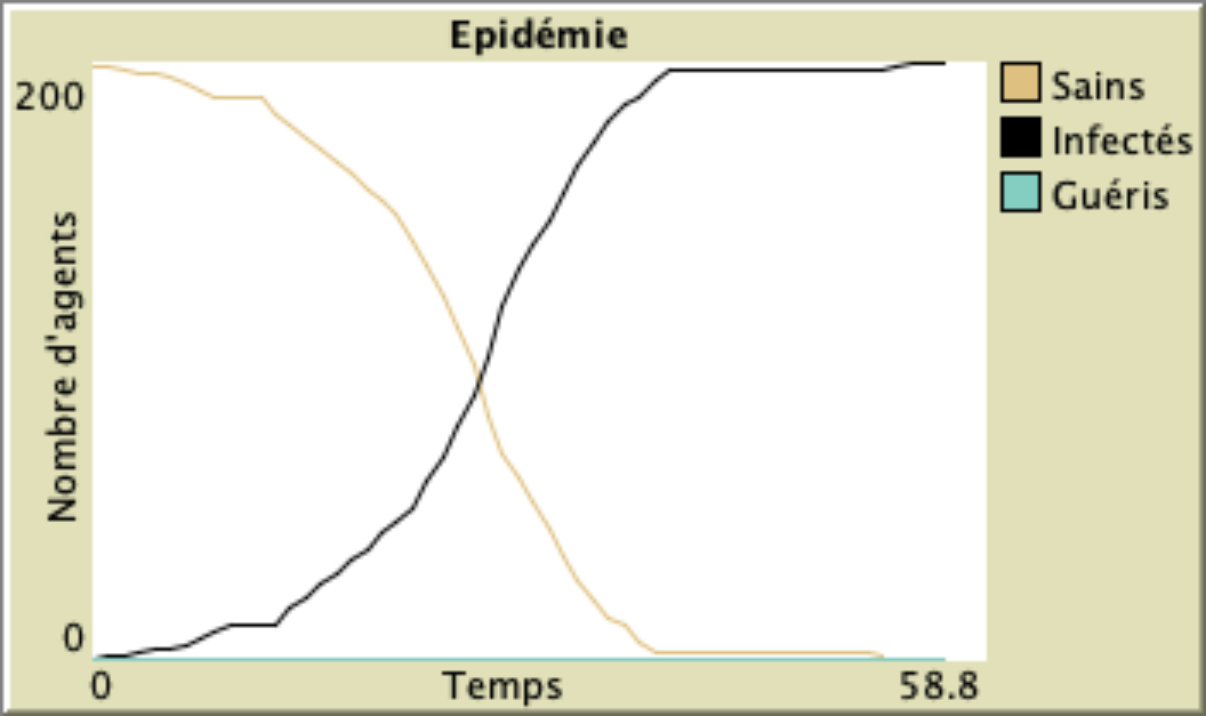
Le “small world”, tel que nous l’avons construit ici, est un hybride entre le réseau aléatoire et le réseau régulier à forte densité locale. La vitesse de propagation du virus y est donc intermédiaire : plus lente qu’avec le réseau aléatoire mais beaucoup plus rapide qu’avec le réseau régulier à forte densité locale. Comme dans ce dernier, la maladie se répand d’abord dans le groupe d’amis du premier agent infecté, puis elle s’y retrouve piégée jusqu’à ce qu’elle infecte un autre groupe d’amis dans le cercle grâce à un lien “passerelle”. Elle peut alors rapidement se propager dans un nouveau groupe d’amis, s’étendre et ainsi de suite jusqu’à contaminer tout le monde.
NB : Il a été démontré que les résultats d’un modèle peuvent varier en fonction de la méthode de construction du “small world” (voir (6)), ici nous avons utilisé celle proposée par Duncan Watts et Steven Strogatz (7).
Formes des réseaux et confinement
Le confinement modifie la forme de notre réseau social. Il est difficile de dire exactement comment et cela fait l’objet d’autres questions traitées ou en cours de traitement. En effet, il faudrait notamment prendre en compte la fréquence avec laquelle un lien donne lieu à une interaction physique et différencier les types de liens : amoureux, familiaux, amicaux, professionnels, éphémères etc.
Réduire les contacts
Ici, nous gardons notre hypothèse de base qu’un lien donne systématiquement lieu à une interaction physique et qu’il n’y pas différents types de liens ; Dans ce cadre là, on pourrait voir le confinement comme un dispositif qui réduit le nombre de liens en interdisant ou limitant certaines activités comme les transports en commun, le travail présentiel, les sports collectifs, les loisirs, les apéritifs chez les amis etc. Dans cette hypothèse, nous allons partir du réseau “small world”, qui reproduit, comme nous l’avons expliqué, des caractéristiques importantes d’un réseau social humain (7), et couper un certain pourcentage des liens.
Illustration : “small world” avec 10 amis en moyenne par agent au départ et une probabilité de transmission de la maladie de 5%. Nous regardons ce qui se passe quand le confinement réduit les interactions de 70, 75, 80, 85 et 90% (de gauche à droite).
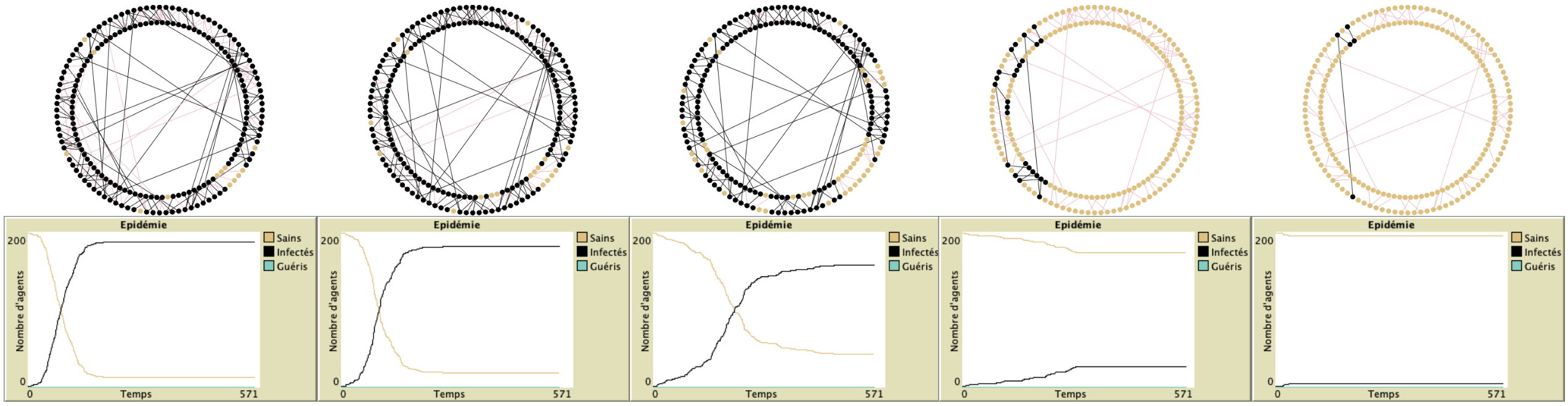
On observe qu’avec le confinement le nombre total de personnes ayant contracté la maladie à la fin de la simulation diminue. En effet, en coupant des liens certains agents se retrouvent coupés du réseau dans lequel se trouve le premier infecté : le confinement peut créer des sous-réseaux indépendants les un des autres, on parle de graphes non-connexes. Ces agents n’attraperont jamais, dans le modèle, la maladie.
Mais même avec des réductions de 80% du nombre de liens, il ne s’agit, la plupart du temps, que de quelques individus qui sont épargnés. Ce qui veut dire que même en lui enlevant aléatoirement 80% de ses liens, notre réseau “smallworld” avec 10 liens par agent, qui a des caractéristiques proches du réseau social humain, continue de connecter la majorité de la population ! Or une étude menée aux États-Unis (8), durant le confinement, montre qu’en moyenne ce dernier réduit les interactions de ”seulement” 70%. Donc il y a fort à parier que le confinement n’arrivera pas à couper suffisamment de liens pour isoler complètement du virus une partie importante de la population. En revanche, on voit que réduire le nombre de liens ralentit fortement la vitesse de propagation de la maladie, ce qui est l’objectif du confinement (voir question 6, 9 et 13 notamment). En effet, dans le modèle moins de liens veut dire moins d’interactions journalières et donc moins de chance pour le virus de contaminer des agents chaque jour.
Gagner du temps ?!
Il devient alors intéressant ici de lever une hypothèse qui est faite depuis le début de cette question et faire en sorte que les personnes infectées guérissent enfin ! En effet si le confinement ralentit la propagation du virus et qu’ainsi le virus finit par progresser moins rapidement que les individus infectés ne guérissent, il peut être stoppé avant de contaminer tout le monde. Dans la suite nous supposerons qu’un agent reste contagieux durant 21 jours ce qui est raisonnable au vu des données sur la maladie.
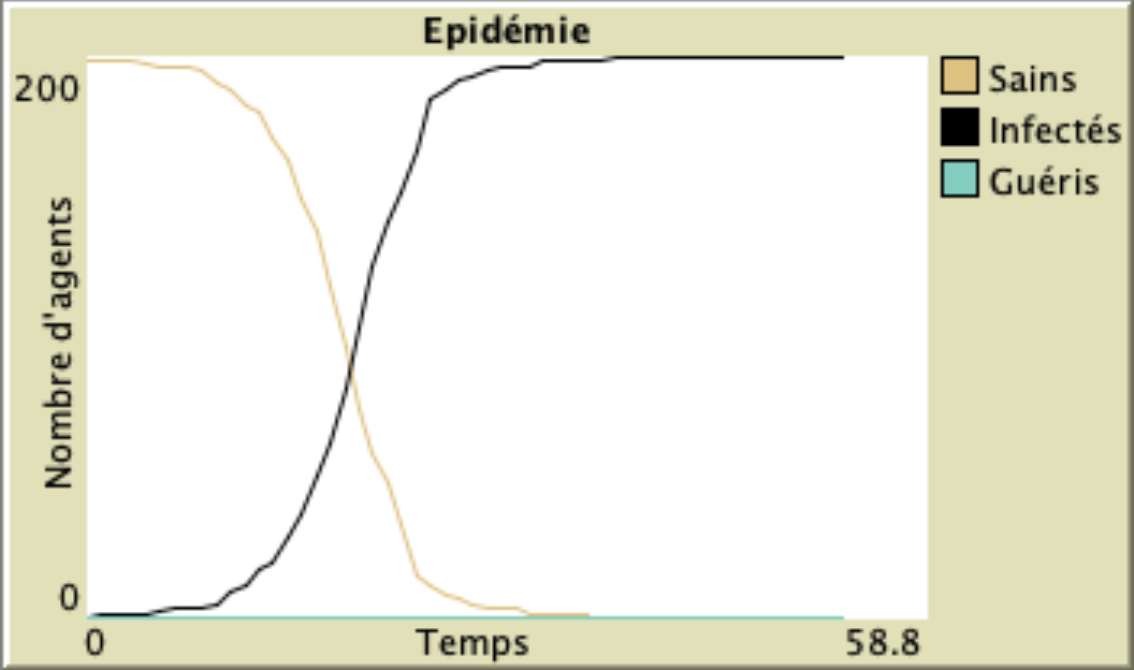
Illustration : probabilité de transmission de la maladie de 5%, “small world” avec 10 liens par agents et pas de confinement.

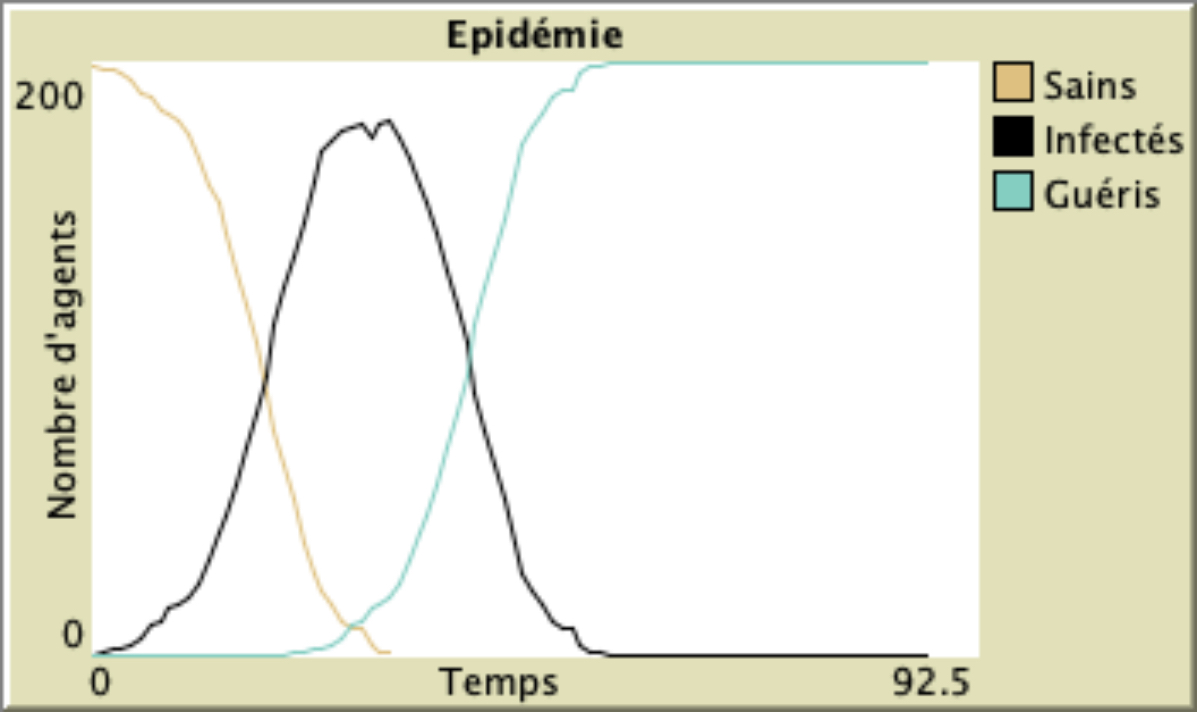
Illustration : probabilité de transmission de la maladie de 5%. Même “small world” que dans l’illustration précédente (10 liens par agents) mais avec un confinement qui couperait 70% des liens existants.

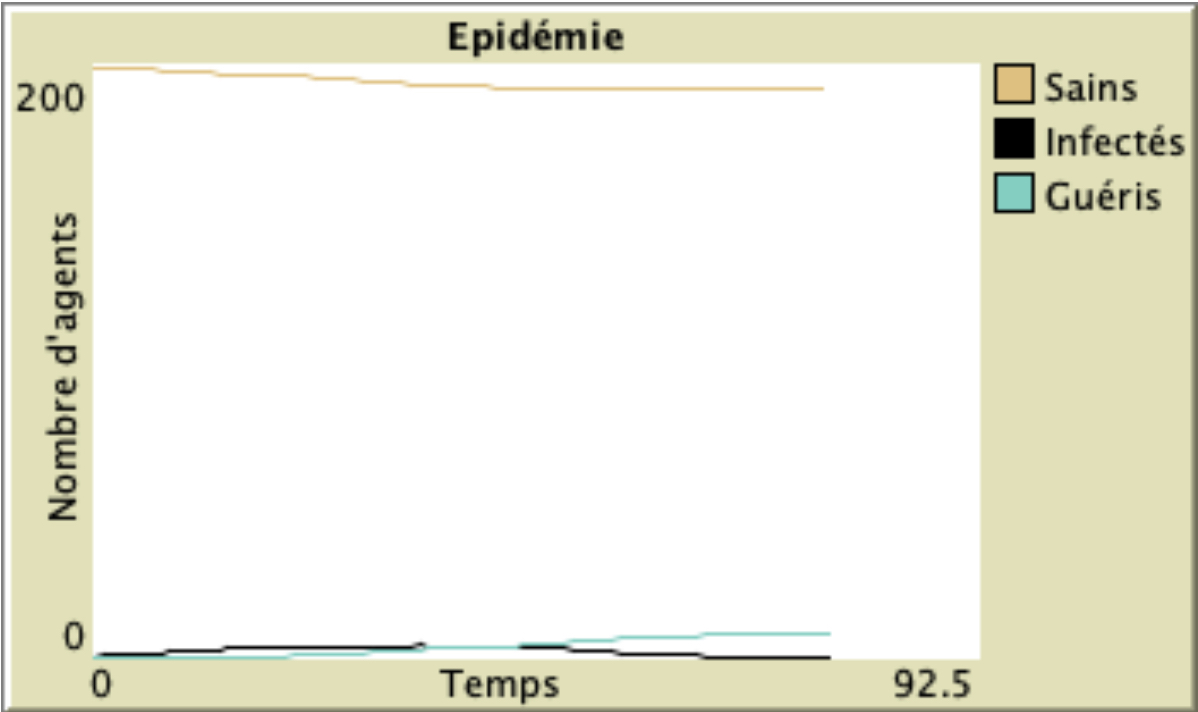
Sans réduction du nombre d’interactions la maladie se propage trop rapidement pour être stoppée et tout le monde finit pas avoir la maladie dans le modèle. Avec 70% de réduction, la vitesse de propagation diminue suffisamment pour que la maladie puisse être stoppée : seulement une poignée d’agents dans cet exemple a été infectée.
Et si la contagiosité augmente ?
Bien sûr ces résultats vont dépendre de la durée de contagiosité et de la probabilité de transmission. Dans un autre exemple ci-dessous, on fait varier la probabilité de transmission de 3 à 7% avec toujours une période de contagiosité de 21 jours. On observe de grandes différences, pour une transmission de 3% le virus est stoppé rapidement et peu de personnes sont contaminées par contre avec une probabilité de transmission de 7% près de 90% des agents finissent par avoir été infectés.
Illustration : “small world”, avec 3 liens par agent en moyenne (par l’effet du confinement). De gauche à droite la probabilité de transmission varie de 3% à 7% (3, 4, 5, 6 et 7%).
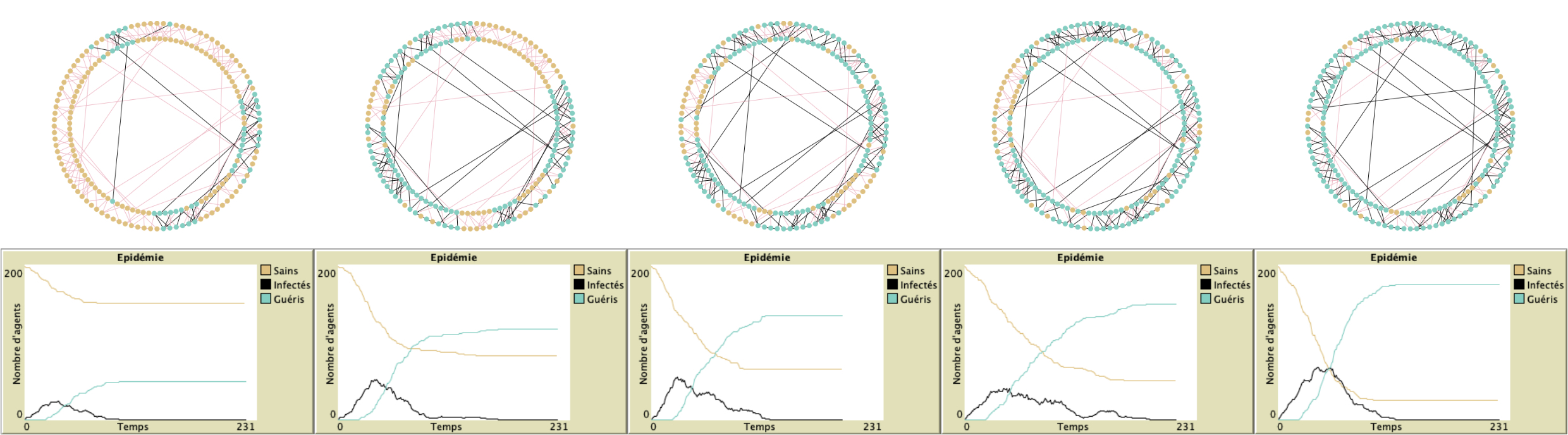
Se confiner autrement, une bonne idée?
Avant de conclure cette question on peut encore regarder ce qui se passe quand les individus décident de contrevenir au confinement et s’organisent en formant des groupes étendus et clos et en limitant au maximum les contacts avec l’extérieur du groupe (exemple des familles avec enfants, parents, oncles, tantes, et grand-parents qui vivent proches les uns des autres et souhaitent continuer de se voir comme avant le confinement).
Illustration : groupes clos de 12 agents sans contacts avec l’extérieur. La probabilité de transmission est toujours de 5%. Un seul groupe est touché, celui de l’agent “zéro” et la maladie est stoppée.

Illustration : groupes clos de 12 agents avec 10% des agents qui ont des contacts à l’extérieur de leur groupe (pour des achats de première nécessité, le travail etc.). La probabilité de transmission est toujours de 5%. Le virus se répand rapidement dans le premier groupe car tout le monde y interagit avec tout le monde. Puis lentement il passe de groupe en groupe. Sa propagation semble tout aussi rapide que pour le réseau aléatoire car dès que le virus rentre dans un groupe, il touche rapidement un grand nombre de personnes. Bien que se répandant rapidement, il épargne tout de même dans cette configuration de réseau une partie de la population qui est dans des groupes complètement séparés des autres.

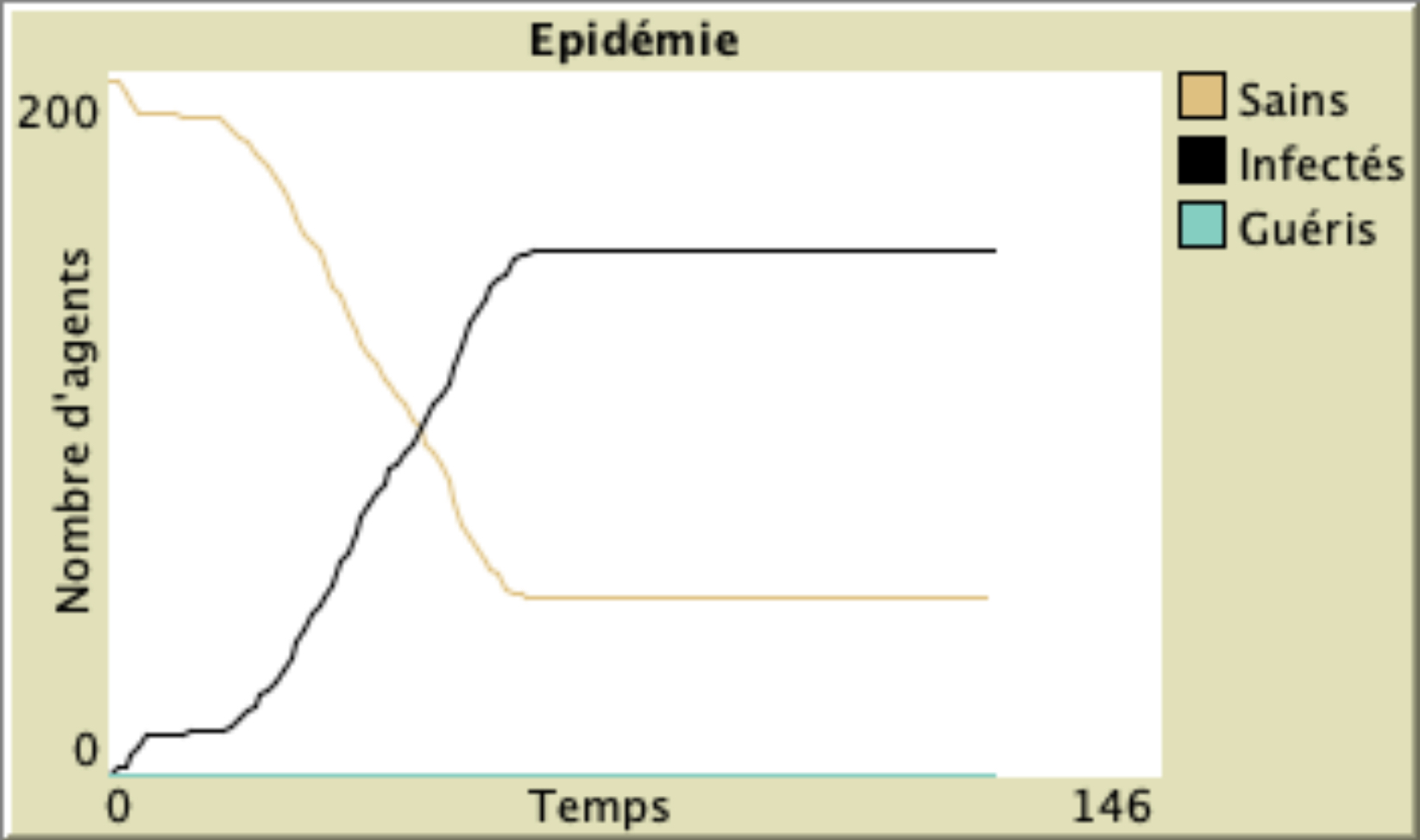
Illustration : groupes clos de 12 agents avec 20% des agents qui ont des contacts à l’extérieur de leur groupe. La probabilité de transmission est toujours de 5%. Le virus se répand très rapidement et touche presque toute la population.

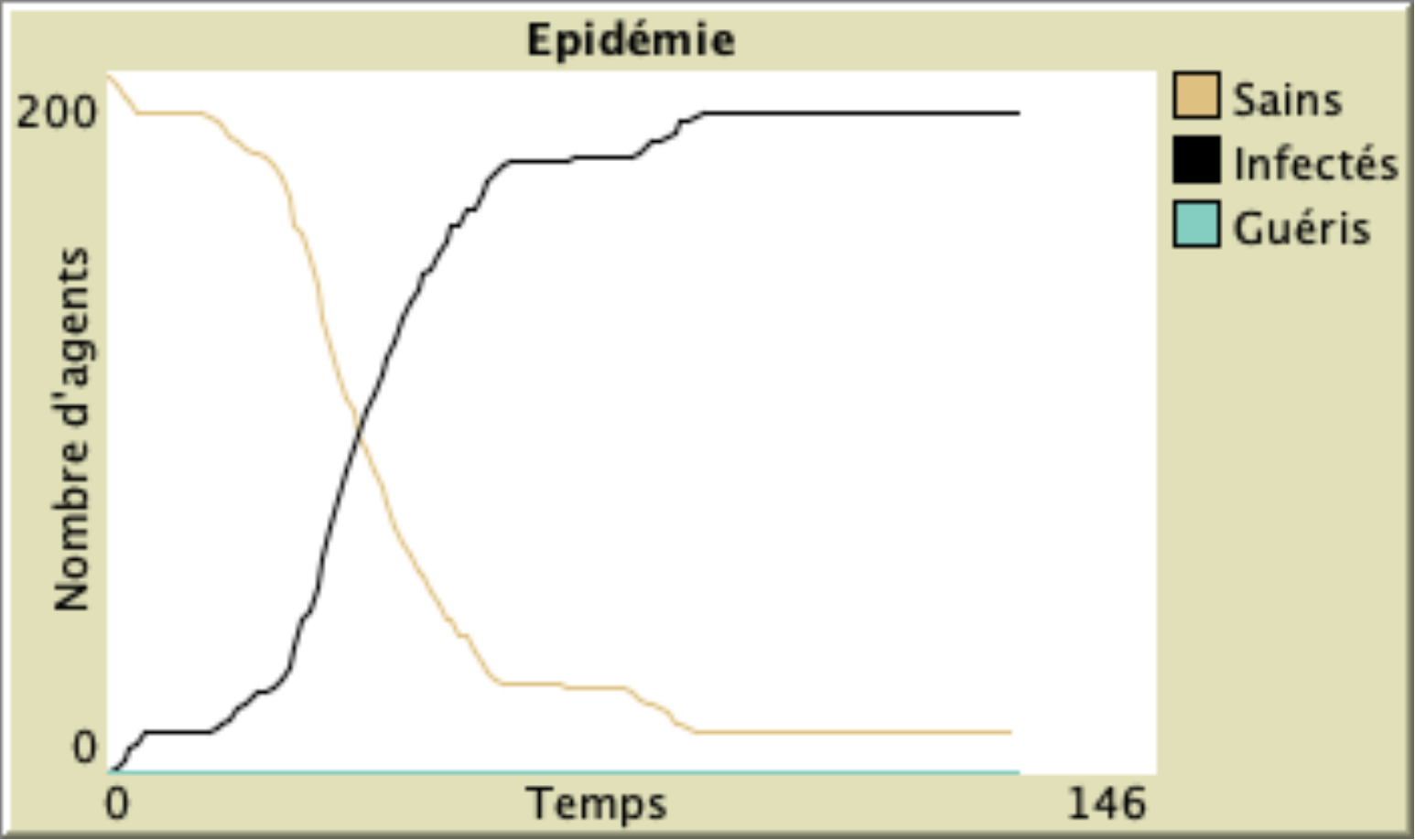
L’organisation en groupes clos s’avère très efficace : elle arrive à stopper la maladie où la configuration en “small world” ne fait que la ralentir. Cependant cela vient au prix d’une hypothèse forte : la parfaite autarcie des groupes. Dès que cela n’est plus vrai, dans le modèle à partir de 10% d’agents qui auraient des contacts avec l’extérieur, le virus se propagerait très rapidement, même s’il épargnerait une partie de la population.
Conclusion
La forme du réseau a une importance dans la propagation du virus et peut contribuer à ralentir ou accélérer la progression de la maladie. Dans le modèle, même si le confinement ne semble pas permettre de complètement isoler une partie de la population du virus, il permet de ralentir suffisamment sa progression et donc de le stopper : le nombre de guérisons devenant rapidement supérieur au nombre de nouveaux cas.
Jouer avec le modèle
Si la fenêtre du simulateur est tronquée à l’affichage, il vous suffit d’effectuer un zoom arrière
Simuler l’impact de la forme du réseau social sur la courbe épidémique
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.
Références Bibliographiques
(1) Mossong et al. “Social contacts and mixing patterns relevant to the spread of infectious diseases.” ( PLoS Med., 2008)
(2) DeStefano et al. “ Factors Associated with Social Contacts in Four Communities During the 2007 2008 Influenza Season.” (Epidemiology & Infection 139 (8): 1181–90, 2011)
(3) Feehan & Cobb. “Using an Online Sample to Estimate the Size of an Offline Population.” (Demography 56 (6): 2377–92, 2019)
(4) Béraud et al. “The French connection: the first large population-based contact survey in France relevant for the spread of infectious diseases.” (PloS one 10.7, 2015).
(5) Guare, J. “Six Degrees of Separation: A Play” (Vintage Books, New York, 1990)
(6) Thiriot, S. “Small world is not enough: Criteria for network choice and conclusiveness of simulations” (JASSS, 2010)
(7) Watts & Strogatz. “Collective dynamics of ‘small-world’ networks” (Nature, 1998)
(8) Feehan and Mahmud. “Quantifying interpersonal contact in the United States during the spread of COVID-19: first results from the Berkeley Interpersonal Contact Study” (preprint, 2020)