La question 8 expose de manière théorique les mécanismes qui concourent à la construction de l’immunité collective et à son fonctionnement en posant comme hypothèses que l’immunité individuelle est instantanée, complète et permanente. La réalité est souvent plus complexe, en particulier en ce qui concerne la COVID-19 car on a encore très peu d’informations sur l’immunité potentielle suite à la maladie (début et durée de cette immunité en particulier), même si des études sont menées partout dans le monde pour pouvoir apporter des réponses sur ce sujet. Le taux d’immunité collective indique la proportion minimale de personnes qui doivent être immunisées pour que l’ensemble de la population soit protégé, un pathogène (bactérie ou virus par exemple) ne pouvant pas se propager s’il ne rencontre pas de personnes saines. Le taux d’immunité collective varie selon les pathogènes et on pense que pour le SARS-CoV-2 il est autour de 60%. Vouloir atteindre 60% d’immunité dans la population en attendant l’arrivée d’un vaccin relève d’une stratégie à haut risque. En effet, en France, cela représenterait environ 40 millions de personnes ayant été contaminées par le virus, et donc des décès qui se compteraient par centaines de milliers potentiellement.
Pour atteindre le taux d’immunité collective dans la population et au regard de l’adoption d’une stratégie de confinement général pratiquée dans de nombreux pays, il peut être envisagé de procéder “par à-coups”, selon une succession de phases de confinement et de déconfinement, pour parvenir progressivement jusqu’à ce taux : confiner la population dès que le nombre de personnes contaminées dépasse un certain seuil, puis déconfiner dès qu’on repasse en-dessous du seuil, mais quelle valeur de seuil choisir ? Et le confinement doit-il concerner uniquement les personnes vulnérables, les personnes malades ou la population générale ? Outre ces questions pratiques, en procédant de cette manière on prend également le risque (du point de vue sanitaire) de dépasser largement le taux d’immunité collective visé par effet boule de neige : lorsque le confinement débute, de nouveaux cas vont encore se déclarer (notamment les personnes encore en phase d’incubation), et si on ne confine pas l’ensemble de la population, les personnes asymptomatiques continueront de propager le virus sans le savoir.
On pourrait intuitivement penser que plus la proportion de personnes immunisées est grande dans la population mieux c’est, mais plus de personnes immunisées impliquent plus de personnes malades avant d’être immunisées (étant donné qu’on ne dispose pas encore d’un vaccin), et donc plus de cas graves qui risquent de surcharger le système de soin et qui entraînent des décès supplémentaires qui auraient pu être évités. Vouloir atteindre le taux d’immunité collective tout en s’assurant qu’il n’y ait pas de saturation du système de soin est une tâche extrêmement complexe (cf Q7). En effet, même si les mesures barrières sont efficaces pour réduire la transmission du virus à l’échelle globale, il n’est pas possible de contrôler précisément cette réduction pour faire en sorte que le virus “circule mais pas trop”. De plus, elles ne permettent absolument pas de contrôler la gravité de l’infection.
Sachant que les mesures barrières sont appliquées pour limiter la transmission (masques, distanciation physique et sociale, etc.), la question qui se pose alors est : à quel(s) moment(s) de l’épidémie faut-il mettre en place un confinement, et selon quelles modalités (isolement ciblé des personnes symptomatiques ou confinement général de la population), pour parvenir à atteindre le plus précisément possible 60% de personnes immunisées dans la population à la fin de l’épidémie ?
Dans le modèle que nous proposons, nous avons choisi de tester et de comparer l’efficacité de trois stratégies largement utilisées dans le monde pour contenir l’épidémie : la protection personnelle et des autres par le port du masque, l’isolement ciblé des cas symptomatiques et le confinement généralisé de la population.
Description du modèle
Caractéristiques de la population
Nous avons simulé une population de 5 000 individus. Les individus de notre population peuvent se trouver dans l’un de cinq états distincts vis-à-vis du virus, récapitulés sur le schéma ci-dessous :
- Sain : n’ayant jamais été infecté, et donc non immunisé ;
- En incubation : infecté par le virus mais pas encore malade (durée moyenne de 6 jours) ;
- Asymptomatique : malade mais ne présentant aucun symptôme (30% des cas ; durée moyenne de 21 jours) ;
- Symptomatique : malade avec des symptômes (70% des cas ; durée moyenne de 21 jours). 5% des malades symptomatiques présentent une forme sévère de l’infection, qui correspond au besoin d’une admission en service de réanimation ;
- Guéri : immunisé et ne pouvant plus être contaminé.
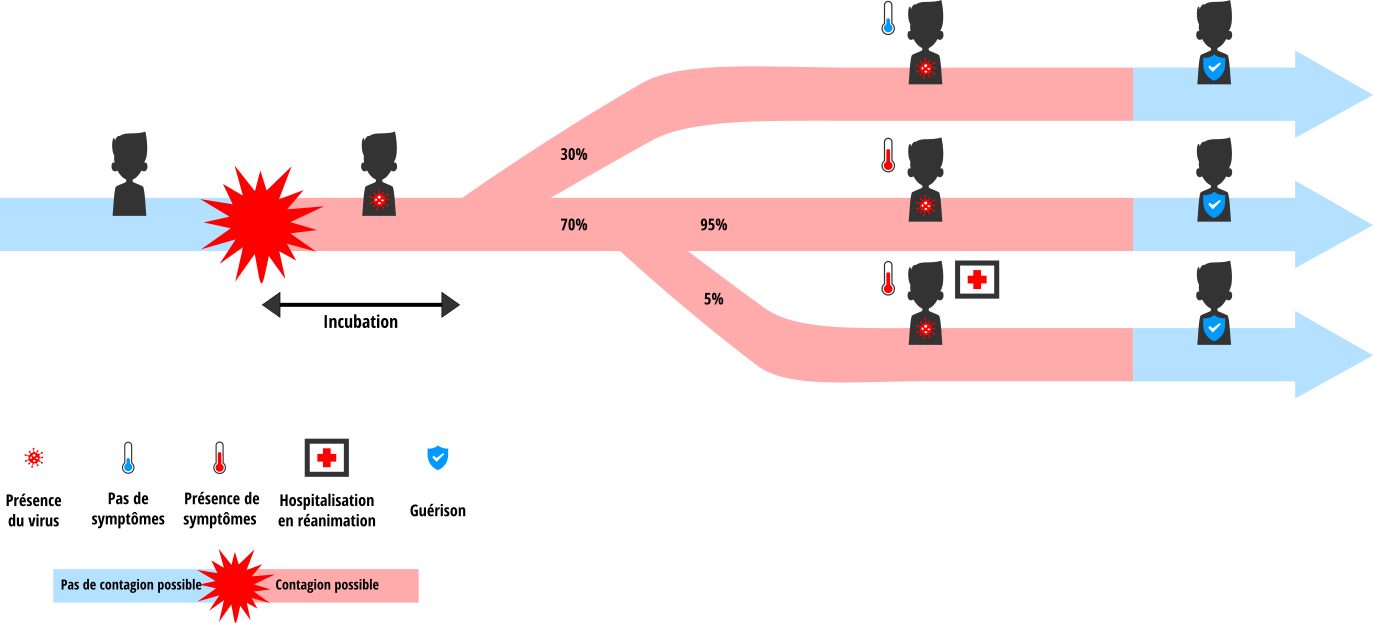
Lors de leurs déplacements dans le monde de simulation, les individus peuvent entrer en contact les uns avec les autres. Les personnes infectées (en incubation, asymptomatiques ou symptomatiques) sont toutes contagieuses et donc susceptibles de transmettre le virus aux individus sains avec qui elles sont en contact.
Stratégies de réduction de la transmission dans notre modèle
Dans le modèle, nous avons introduit trois stratégies visant à réduire la transmission du virus dans la population. Celles-ci seront testées séparément puis conjointement avec une logique de progression dans les restrictions des libertés individuelles : port du masque d’abord, suivi de l’isolement ciblé des personnes symptomatiques, puis du confinement général.
-
Stade 1 : la stratégie de port du masque est modélisée par la diminution du risque de transmission du virus par les personnes contagieuses lors d’un contact : le risque est deux fois moins élevé si la personne contagieuse porte un masque. Dans le modèle, vous pouvez choisir la proportion de personnes (quel que soit leur statut vis-à-vis du virus) qui portent un masque lors de leurs déplacements via le paramètre proportion-masques. Nous supposons ici que les masques sont disponibles en quantité suffisante pour toute la population dès le début de l’épidémie. Nous avons choisi de modéliser uniquement la réduction de la contagiosité et non l’effet protecteur du masque pour les personnes saines, dans un souci de simplification du modèle.
-
Stade 2 : la stratégie de l’isolement ciblé consiste à mettre en quarantaine les personnes symptomatiques dès le début de leurs symptômes, afin de leur éviter de contaminer d’autres personnes. Elles restent en quarantaine jusqu’à leur guérison, sans aucun contact possible avec le reste de la population. Cela suppose que tous les cas symptomatiques sont identifiés et confirmés, et qu’ils sont complètement isolés, dans une chambre d’hôtel par exemple. Dans le modèle, on déclenche cette stratégie lorsque la proportion de personnes symptomatiques dans l’ensemble de la population dépasse un seuil que vous pouvez fixer via le paramètre seuil-confinement-cible. On suppose donc ici que les tests sont immédiatements disponibles et toujours justes, et que tous les cas confirmés disposent d’un lieu d’isolement. Une stratégie similaire a été testée indépendamment dans la Q6, alors que la Q13 évoque les pays ayant choisi cette stratégie.
-
Stade 3 : enfin, la stratégie de confinement général consiste à isoler l’ensemble de la population pendant une durée donnée pour réduire au maximum la transmission du virus. Pour prendre en compte les déplacements nécessaires (les emplois essentiels, faire les courses, sortir son chien, etc.) et le non-respect de cette consigne par une partie de la population, on considère dans le modèle que 20% des personnes ne présentant pas de signes de la maladie se déplacent (i.e. les personnes susceptibles, asymptomatiques ou guéries) chaque jour. Dans le modèle, cette stratégie est déclenchée lorsque le nombre de cas sévères dans la population (soit 5% des cas symptomatiques) dépasse la capacité d’accueil des services de réanimation (3 lits pour 1000 personnes en France). À partir de ce seuil, un confinement général d’une durée fixée par le paramètre duree-confinement-general entre en vigueur.
Après la fin du confinement général, on repasse au stade 2 d’isolement ciblé. Si le système de soin est à nouveau saturé, une nouvelle période de confinement général sera enclenchée. Lorsque la proportion de cas symptomatiques repasse en-dessous du seuil défini, on redescend au stade 1, avec comme unique mesure de réduction de la transmission le port du masque. La simulation s’arrête lorsque le virus ne circule plus.
À vous de jouer
Si la fenêtre du simulateur est tronquée à l’affichage, il vous suffit d’effectuer un zoom arrière
Atteindre le taux d’immunité collective
Applications
Cas 1 : Seulement masqué tu sortiras
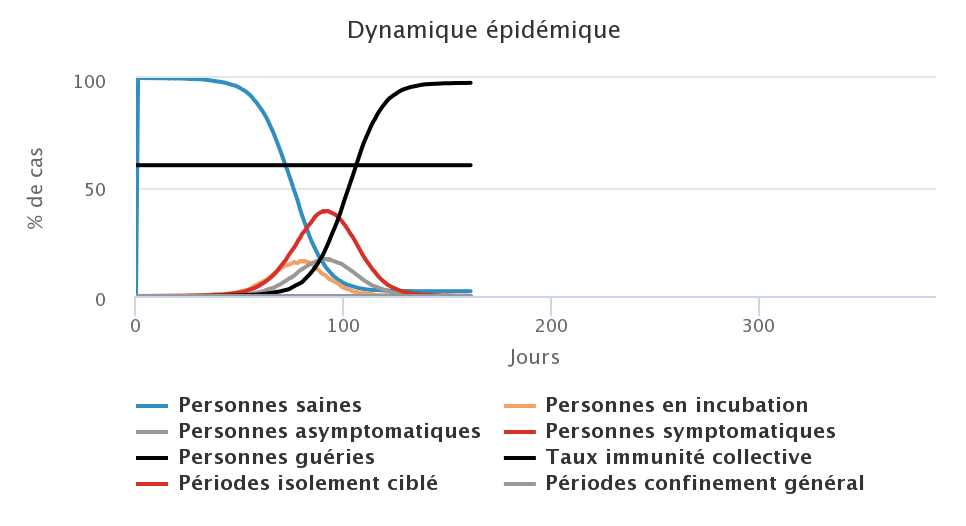
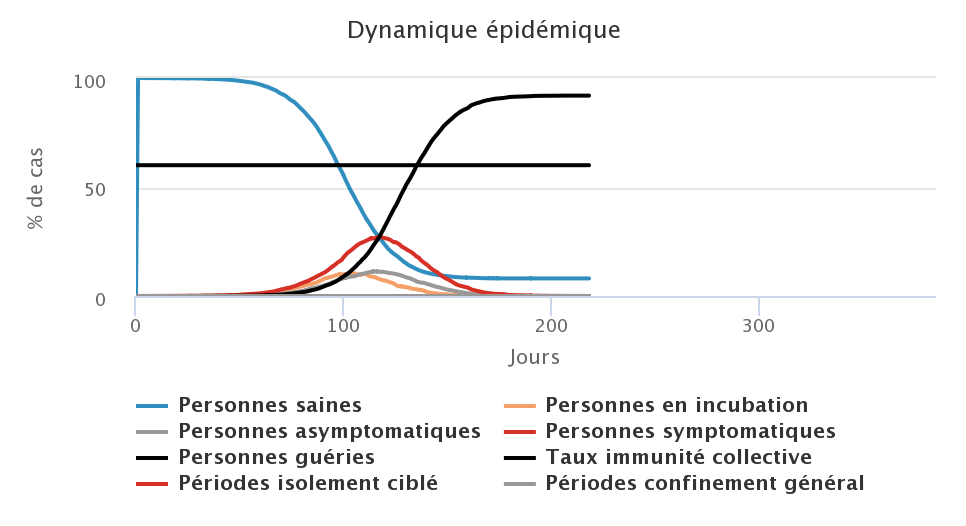
Dans cette première série de simulations, nous testons exclusivement l’effet du port du masque sur la dynamique de l’épidémie, il n’y a pas de confinement. L’hypothèse de base est qu’il doit exister une corrélation négative entre la proportion de personnes portant un masque (quel que soit leur état vis-à-vis du virus) et le nombre de malades. Nous faisons varier cette proportion de 0%, 50%, 75 % et 100% des individus. Sur les figures ci-dessous, la ligne noire horizontale représente l’objectif de 60% de personnes immunisées, nous voulons en être le plus proche possible à la fin de l’épidémie. Rappelons que le port du masque par une personne contagieuse dans ce modèle réduit de moitié la probabilité de transmettre le virus lorsqu’elle est en contact avec une personne saine.
| O% de masques | 50% de masques |
|---|---|
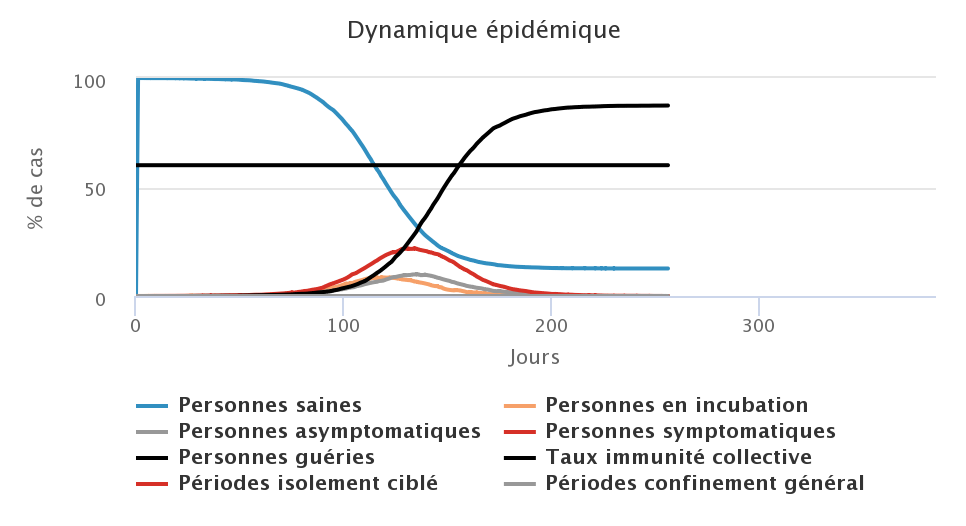
| 75% de masques | 100% de masques |
|---|---|
Cette stratégie est intéressante car elle permet d’aplatir et d’étaler les courbes qui représentent les personnes contaminées, c’est-à-dire les courbes orange (personnes en incubation), grise (personnes asymptomatiques) et rouge (personnes symptomatiques). Par conséquent, on peut s’attendre à ce que les cas graves soient mieux absorbés par le système de santé car étalés dans le temps. Cette stratégie permet également de réduire le nombre total de personnes infectées par le virus au cours de l’épidémie, passant de presque 100% de personnes touchées (figure en haut à gauche), à environ 75% de personnes infectées dans le cas où tout le monde porte un amsque (figure en basà froite). L’effet négatif est que la durée de l’épidémie est allongée lorsqu’aucun effet extérieur n’est pris en compte (climat, mouvements de population pour des vacances ou fêtes religieuses par exemple). Même dans le cas où 100% de personnes portent un masque, la circulation du virus est possible car nous avons considéré que les masques n’étaient pas efficaces à 100% mais à 50% pour réduire la probabilité de contamination.
Cas 2 : Vise, mais bien !
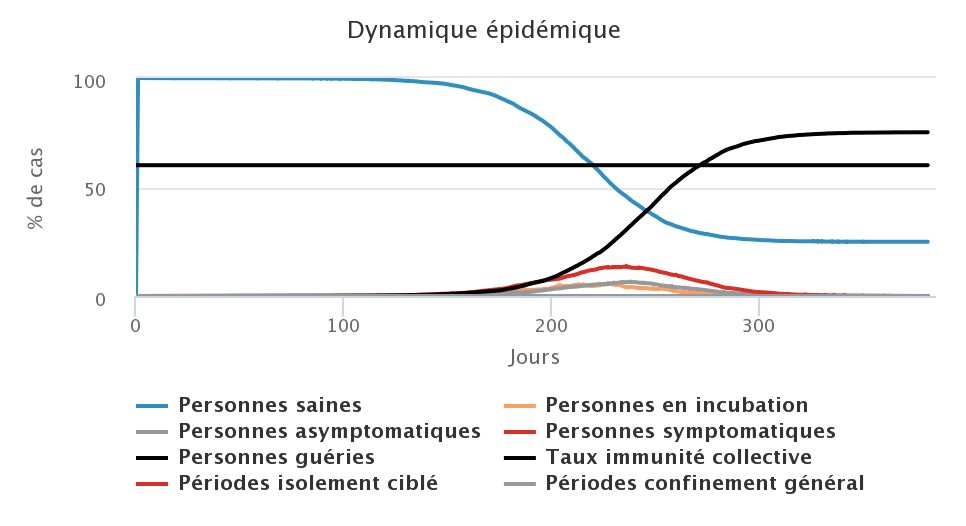
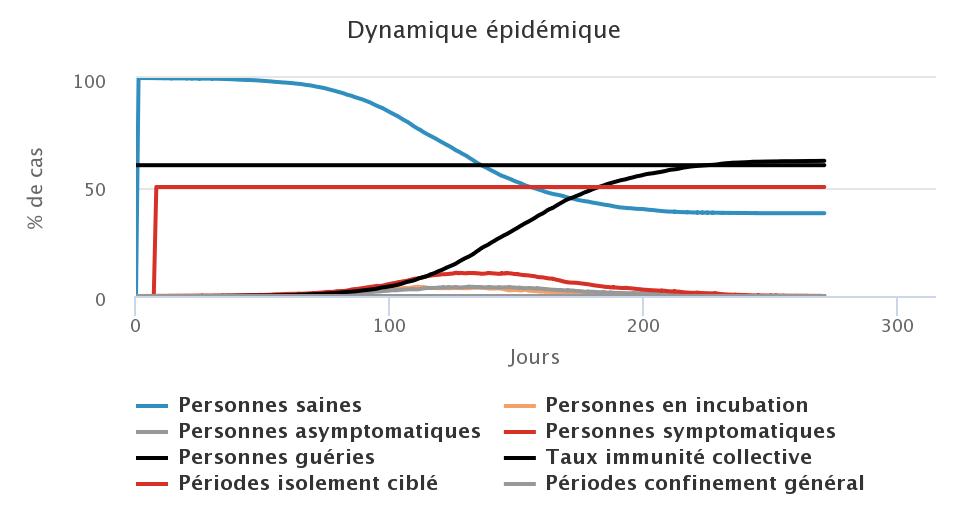
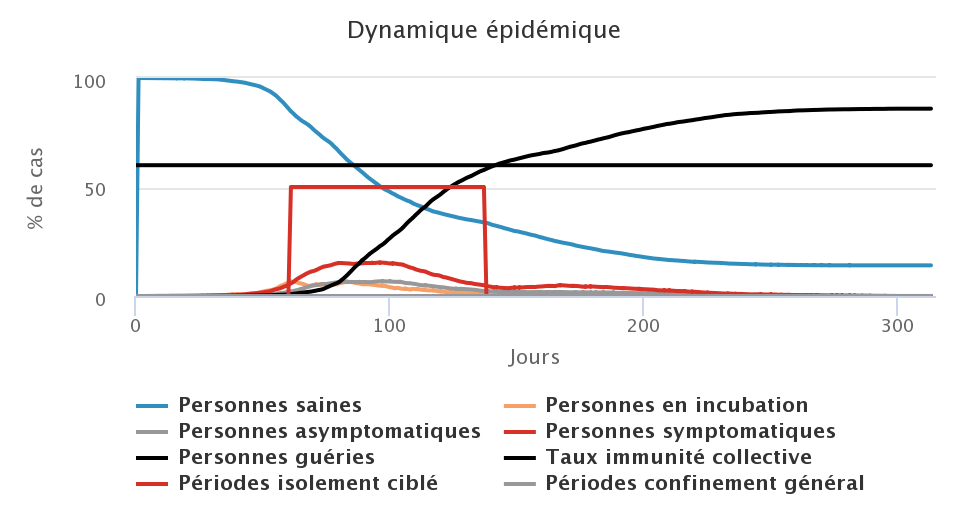
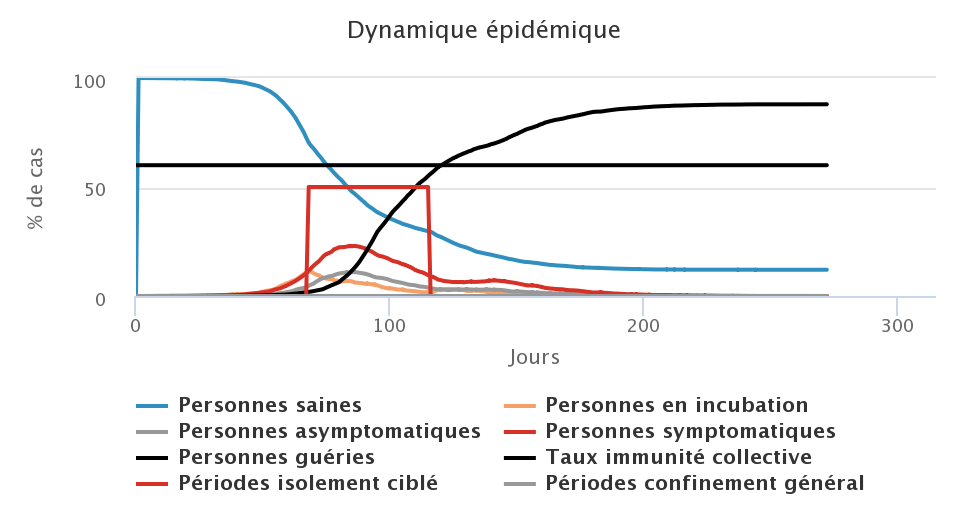
La seconde stratégie que nous avons testée est celle du confinement ciblé. Ici pas de masques, mais on instaure l’isolement complet de toute personne qui présente des symptômes, dès l’apparition de ceux-ci. Cela ne concerne donc pas tous les cas puisque 30% des malades sont asymptomatiques et n’empêche pas non plus la transmission du virus pendant la phase d’incubation, soit avant l’apparition potentielle des premiers symptômes. L’efficacité de cette mesure à un niveau global étant liée à sa date de déclenchement, nous avons testé différents seuils de déclenchement relatifs à la proportion de personnes symptomatiques dans la population : 0% (dès qu’apparaît le premier cas), 5% et 10% de personnes symptomatiques dans la population.
| Seuil à 0% | Seuil à 5% |
|---|---|
| Seuil à 10% |
|---|
Comme le port du masque, cette mesure a un impact positif : si elle est prise très tôt (dès le 1er cas, figure en haut à gauche), elle limite considérablement la circulation du virus et donc la flambée épidémique. La courbe des cas est donc lissée et on se rapproche des 60% de personnes guéries à la fin de l’épidémie, soit le taux d’immunité collective. En revanche, si le confinement ciblé est mis en place plus tard, lorsqu’il y a déjà un certain nombre de personnes infectées dans la population, on observe un plus grand nombre de cas au total (près de 90% de personnes infectées au cours de l’épidémie sur la figure du bas) et une deuxième vague épidémique se produit après la levée du confinement ciblé (même si elle reste relativement faible). Cette seule mesure ne suffit donc pas à contenir l’épidémie puisqu’il ne faut absolument pas rater le début de la vague épidémique et donc la déclencher le plus tôt possible.
Cas 3 : Que plus personne ne bouge !
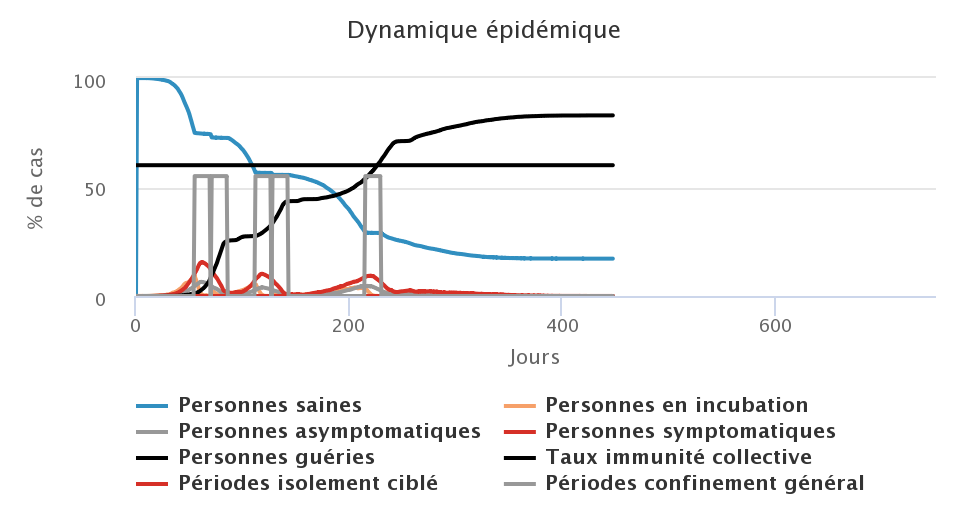
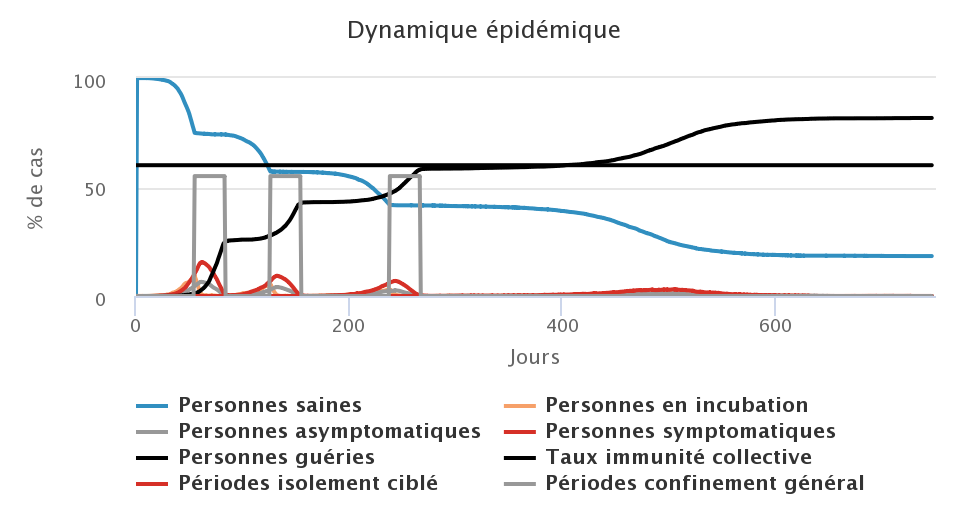
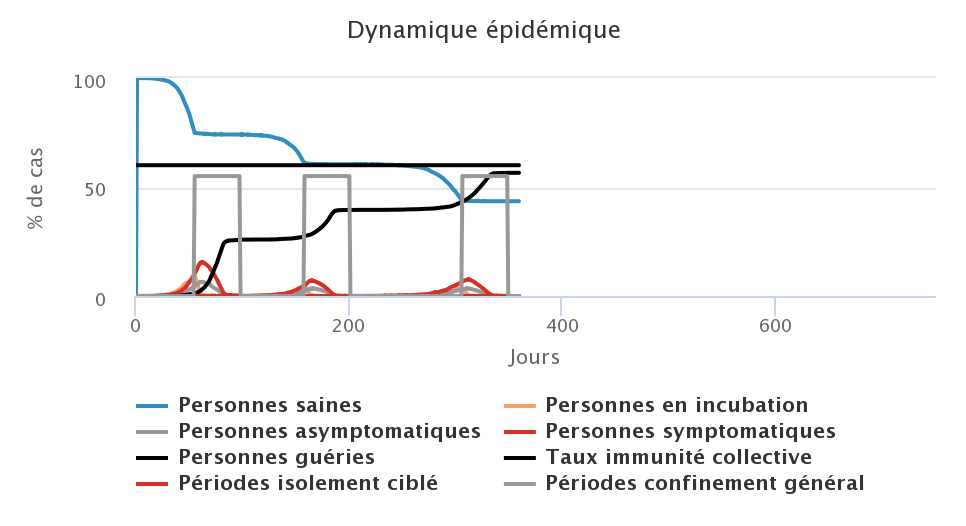
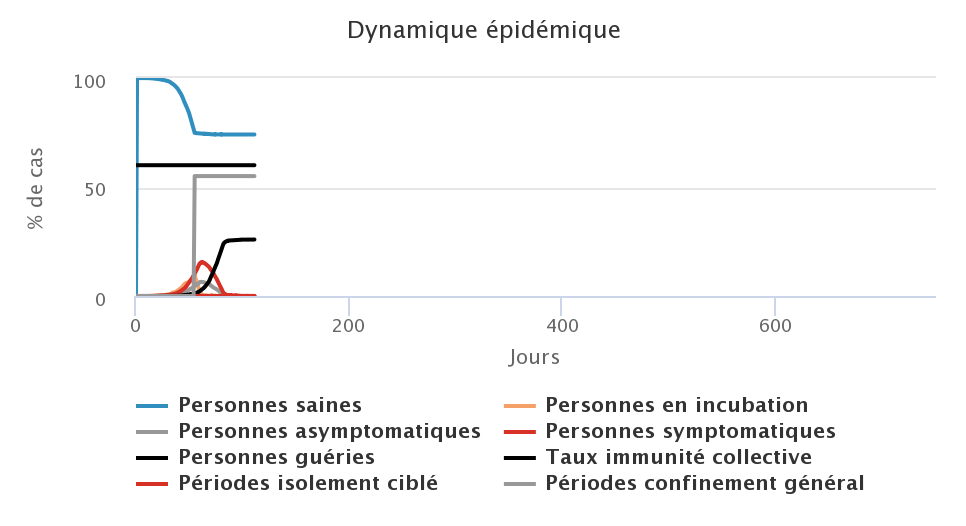
Enfin, nous avons testé la troisième stratégie, celle du confinement généralisé qui consiste à isoler toute la population à partir du moment où le système de soin est surchargé. L’efficacité du confinement est liée à son respect par la population (ici nous supposons que 20% des personnes qui ne présentent pas de symptômes de la maladie se déplacent malgré le confinement) mais aussi à sa durée. Nous avons donc testé un confinement général d’une durée de 2, 4, 6 et 8 semaines. Dans les graphiques ci-dessous, les histogrammes en gris représentent les périodes de confinement général.
| Confinement de 2 semaines | Confinement de 4 semaines |
|---|---|
| Confinement de 6 semaines | Confinement de 8 semaines |
|---|---|
Dans les conditions du modèle, un confinement de 8 semaines (figure en bas à droite) permet de stopper rapidement la progression du virus. Malgré une minorité de personnes en mobilité, et parmi elles des cas asymptomatiques contagieux, l’épidémie est stoppée dans sa progression et plus aucun cas n’est comptabilisé au sortir du confinement. Cependant, dans ce cas là, le taux d’immunité collective n’est pas atteint et si le virus venait à réapparaître dans la population, une nouvelle vague épidémique se produirait. Lorsque la durée du confinement est trop courte au regard des périodes d’incubation et de contagiosité, une phase de stop-and-go se met en place avec des vagues successives de rebond de l’épidémie : avec des confinements de 2 semaines (figure en haut à gauche), on observe ainsi deux fois deux périodes de confinements successifs, puis une dernière période de confinement. Dans les figures présentées ici, la mailleure stratégie semble être celle du confinement de 6 semaines, qui permet de ne pas trop faire durer l’épidémie, de ne pas surcharger le système de soin et d’être le plus près possible du taux d’immunité collective à la fin de l’épidémie.
Cas 4 : Couvre-toi, vise bien et tous aux abris
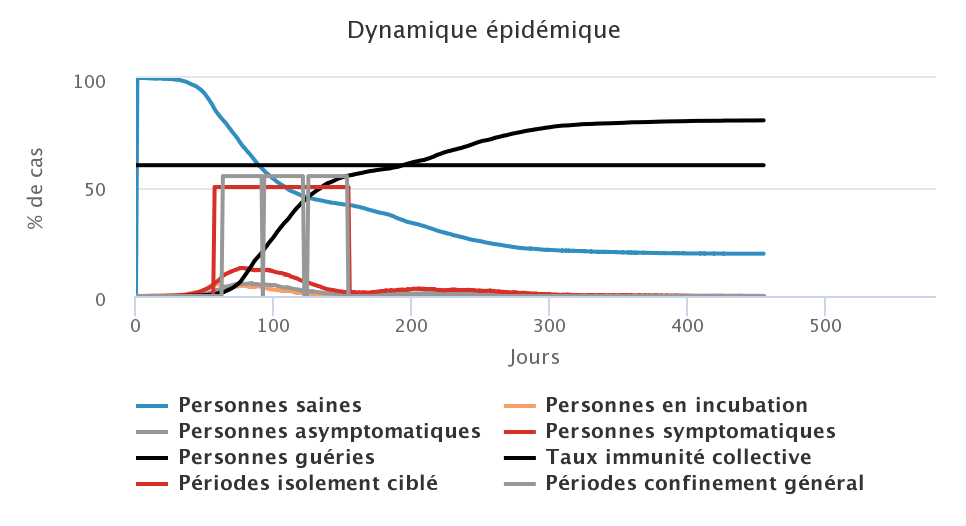
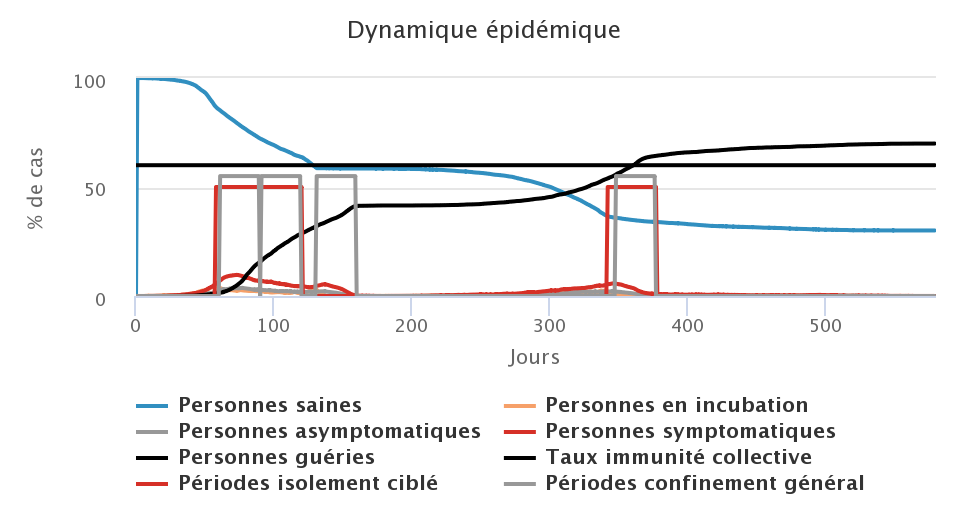
Comme nous l’avons vu dans les trois précédents scénarios, l’application d’une seule stratégie n’a des effets significatifs sur l’épidémie que si elle est appliquée dans des conditions peu réalistes, ou bien elle n’aura que des effets relativement limités. Le scénario qui suit s’intéresse donc à la combinaison de ces trois stratégies sur différents jeux de paramètres. Les trois tactiques ne sont pas appliquées au même moment, puisque le port du masque est mis en place dès le début, suivi de l’isolement ciblé lorsque les cas symptomatiques dépassent un certain seuil. Le confinement général survient enfin lorsque la circulation du virus n’est plus contrôlée au regard de la capacité de charge du système hospitalier. Nous faisons donc varier dans les simulations qui suivent la proportion de la population qui porte un masque (PM), le seuil de déclenchement de l’isolement ciblé (SIC) ainsi que la durée de confinement général (DCG).
| PM 25% ; SIC 5% ; DCG 4 semaines | PM 50% ; SIC 5% ; DCG 4 semaines |
|---|---|
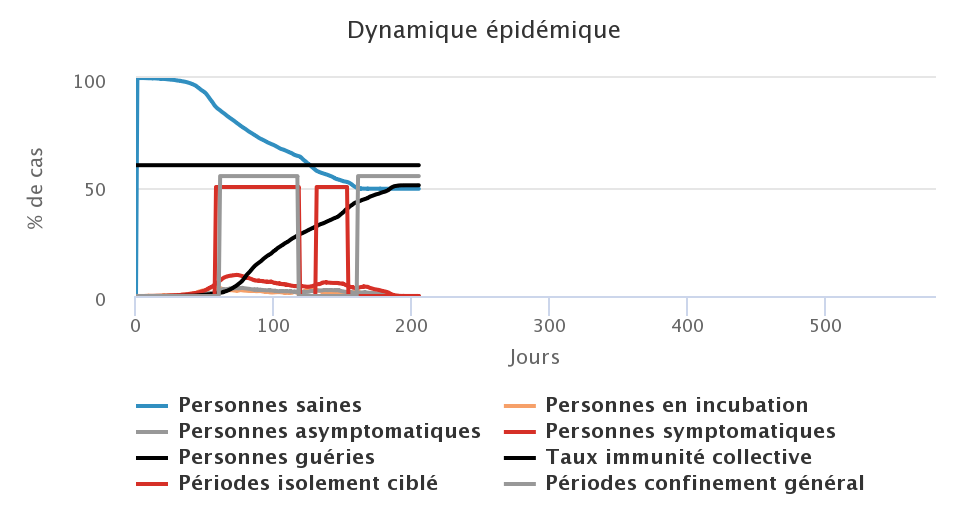
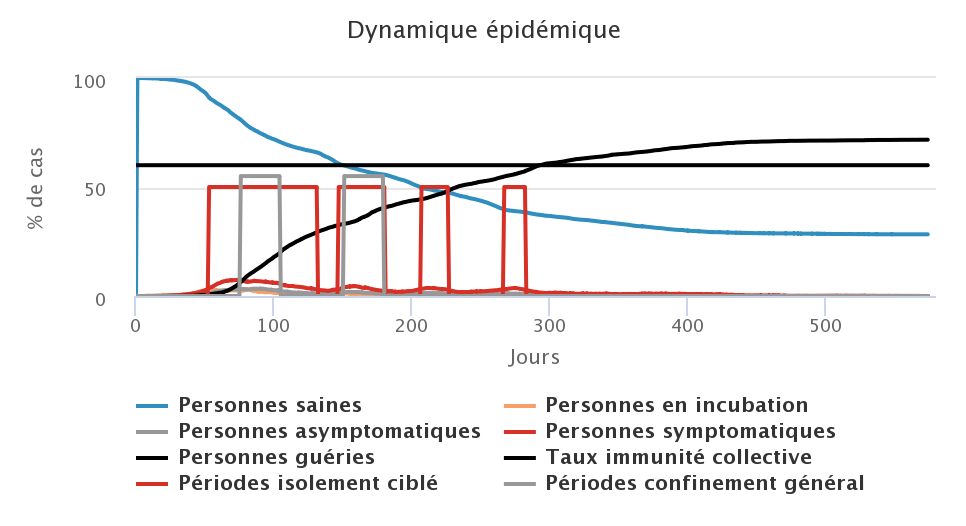
| PM 50% ; SIC 5% ; DCG 8 semaines | PM 50% ; SIC 3% ; DCG 4 semaines |
|---|---|
La première leçon de cette série de simulations est qu’il est complexe de pouvoir identifier les effets d’une mesure particulière lorsque plusieurs sont appliquées au même moment, car ces effets sont interdépendants. La seconde leçon est qu’il est possible de parvenir à peu près au même résultat avec des tactiques différentes. Les quatres simulations montrent ainsi qu’il est possible de parvenir à un taux de personnes guéries à la fin de l’épidémie d’environ 75% avec des valeurs de paramètres très différentes pour chacune des tactiques employées. En revanche, ces choix ont des effets sur ce que doit “subir” la population : de longues périodes de confinement ou un port du masque généralisé.
Recherche de la stratégie optimale
Afin de déterminer la stratégie qui permet d’obtenir le résultat le plus satisfaisant, nous avons exécuté un algorithme d’optimisation sur notre modèle. Cet algorithme simule le modèle un très grand nombre de fois en faisant varier les valeurs des paramètres d’entrée, dans le but d’optimiser les critères qui nous paraissent les plus importants à atteindre à la fin de l’épidémie.
Nous avons fait varier les trois paramètres d’entrée suivants :
- La proportion d’individus qui portent des masques lors de leurs déplacements;
- Le seuil sur la proportion de personnes symptomatiques à partir duquel on déclenche le confinement ciblé de ces personnes ;
- La durée du confinement général lorsqu’il est déclenché.
Dans le but d’atteindre les deux critères de sortie suivants :
- Le nombre minimal de périodes de confinement général ;
- La proportion de personnes immunisées la plus proche possible du taux d’immunité collective de 60%.
Pour une population de 10 000 agents, l’algorithme a trouvé une unique “meilleure” solution pour notre modèle :
- si 93% des gens portent un masque lors de leurs déplacements,
- et que le confinement ciblé démarre à partir de 1,4% de personnes symptomatiques dans la population,
- alors on peut atteindre 60% de personnes immunisées à la fin de l’épidémie sans aucune période de confinement général.
Cette stratégie ne paraît cependant pas très réaliste à mettre en place car elle nécessite une grande quantité de masques disponibles immédiatement et portés par quasiment l’ensemble de la population. Elle nécessite également d’avoir à disposition des tests en nombre suffisant pour pouvoir confirmer tous les cas suspects et les isoler de manière efficace. Au-delà de cette stratégie “idéale” au regard des objectifs et des contraintes, nous allons donc étudier le comportement du modèle dans l’espace de ses paramètres sous contrainte de résultats attendus.
Recherche de tous les paramètres permettant d’arriver à notre objectif
L’algorithme précédent est intéressant pour nous donner une idée de la meilleure stratégie possible, mais il n’est pas forcément facile de mettre en place cette stratégie et nous n’avons pas nécessairement besoin de la meilleure stratégie mais d’une stratégie “suffisamment bonne”. Il est donc également intéressant de savoir quels sont les jeux de paramètres nous permettant d’atteindre une zone que nous jugeons acceptable vis-à-vis de nos critères de sortie (cf plus haut).
Pour cela nous avons utilisé l’algorithme Origin Space Exploration, qui permet de fixer l’espace de sortie que nous jugeons acceptable, puis qui nous fournit l’ensemble des jeux de paramètres d’entrée qui permettent au modèle d’atterrir dans cet espace de sortie à la fin de la simulation. Ici l’espace de sortie acceptable est le fait d’avoir moins de 5 périodes de confinement général et de compter entre 55 et 65% de personnes immunisées à la fin de l’épidémie.
La figure suivante est le résultat produit par l’algorithme OSE : chaque point représente une simulation dont les critères de sortie sont dans la zone acceptable que nous avons définie. Le point rouge en bas à droite dans la zone B représente la “meilleure solution” obtenue par l’algorithme d’optimisation précédent.
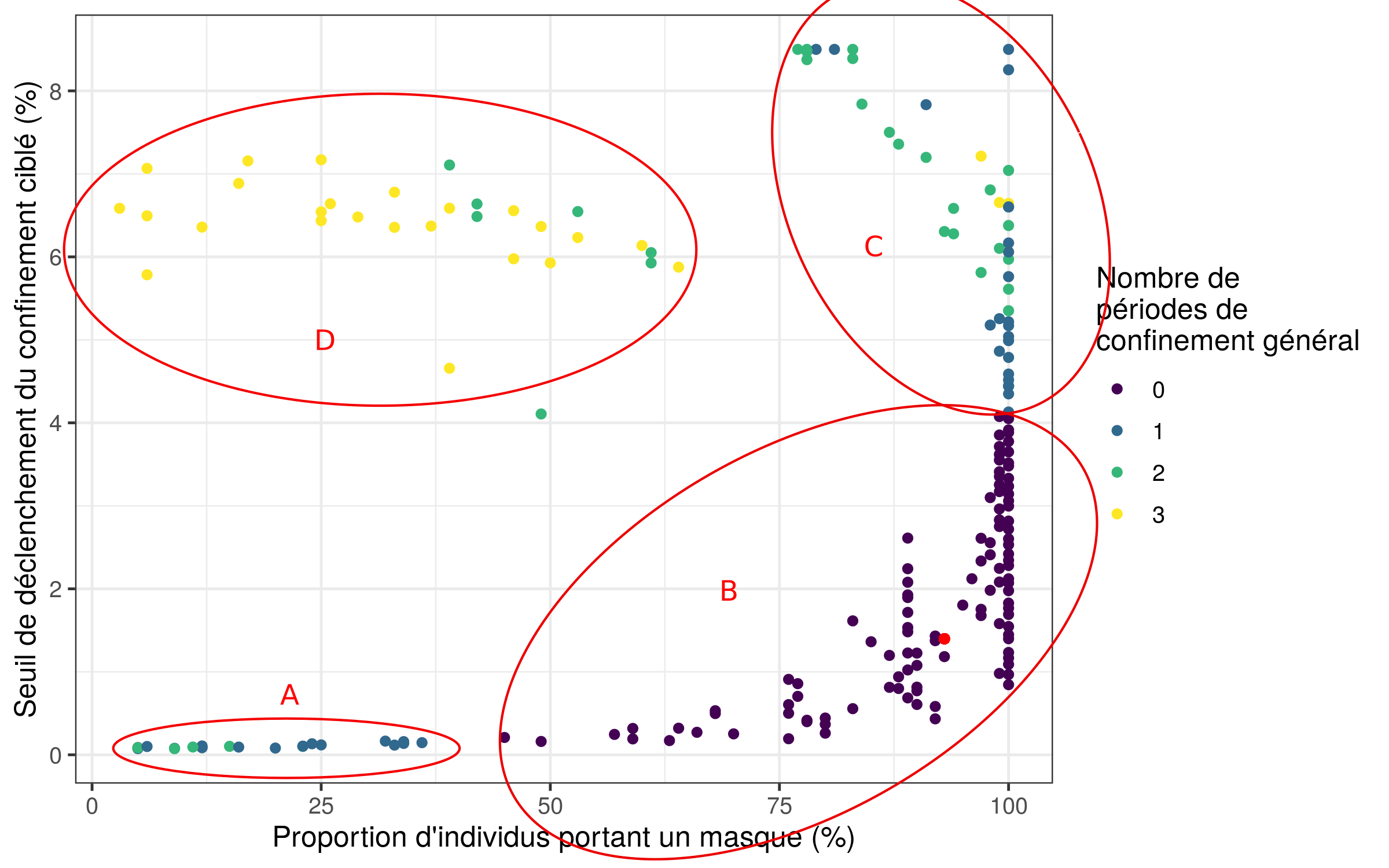
On observe que notre modèle possède plusieurs régimes de fonctionnement :
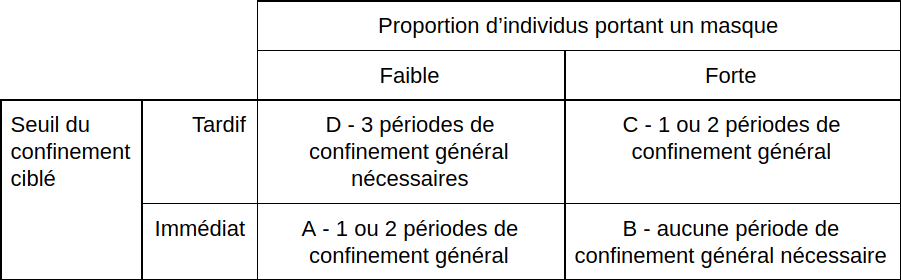
Dans ce modèle, si la solution optimale trouvée précédemment révélait des difficultés pratiques de mise en oeuvre, on peut voir ici qu’il existe d’autres combinaisons de paramètres permettant d’obtenir un résultat semblable, i.e. d’atterrir dans la zone B : pas de nécessité de confinement général tout en atteignant le taux d’immunité collective. Les marges d’action sur le port du masque et le début du déclenchement de l’isolement ciblé sont finalement assez importantes :en testant de manière systématique tous les cas symptomatiques et en les mettant en quarantaine précocement (dès le début de la circulation du virus dans la population), même avec une population en partie réfractaire au port du masque (autour de 50%) on atteint nos objectifs. De même, en l’absence de test au début de la circulation du virus, on peut tout de même atteindre nos objectifs en incitant une majorité de la population (> 90%) à porter un masque. Inversement, la faiblesse du port du masque dans la population et/ou un isolement ciblé tardif (dû par exemple à une insuffisance de tests) peut nécessiter jusqu’à trois périodes de confinement généralisé pour atteindre les objectifs (zone D).
Conclusion
Les ressources disponibles pour lutter contre une épidémie doivent être variées et en quantités suffisantes pour pouvoir faire évoluer la stratégie de lutte contre la progression du virus en période épidémique. Le modèle que nous avons exploré ici illustre bien ce propos, à la fois sur la complémentarité des choix tactiques que sur leurs combinaisons selon le stade de l’épidémie. Les meilleurs résultats que permettent d’obtenir ce modèle se situent en début d’épidémie, cela révèle l’importance d’un système de surveillance performant, d’un système de gestion de crise réactif et d’un système de soin performant.
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.