« Laissez faire, laissez passer, le monde va de lui-même » disait D. de Gournay (économiste qui introduisit la pensée libérale en France au 18ème siècle). Supposons qu’un pathogène (c’est-à-dire une entité qui provoque des maladies, comme un virus ou une bactérie par exemple) contre lequel aucun vaccin ne soit disponible arrive dans un pays. Supposons également qu’aucune mesure de mitigation ne soit mise en place pour limiter sa diffusion : pas de fermeture des frontières, pas de confinement des personnes, pas de dépistage ni de mise en quarantaine des personnes infectées, etc. Alors ce pays, en laissant circuler librement ce pathogène, va adopter, consciemment ou non, la stratégie de l’immunité collective.
L’idée est relativement simple : la plupart des pathogènes qui circulent au sein d’une population immunisent pour un temps donné les personnes qui ont été infectées. Au cours du temps, le pathogène aura donc de plus en plus de difficultés à trouver des hôtes potentiels sur son chemin pour poursuivre sa progression. La population dans son ensemble sera donc immunisée, même si tous les individus ne le sont pas. Lorsque le pathogène disparaît, si la durée de cette immunité acquise est relativement faible (quelques mois ou années) et à la faveur du renouvellement des populations, par les migrations et les naissances, le taux de personnes immunisées dans la population va progressivement diminuer et le risque qu’une ré-émergence du pathogène donne lieu à une épidémie va augmenter.
Il faut donc distinguer le taux de personnes immunisées, qui correspond à la proportion de personnes immunisées dans l’ensemble de la population, et le taux d’immunité collective qui est un seuil, un objectif à atteindre calculé selon les caractéristiques propres au pathogène en question. Le taux d’immunité collective est un indicateur statistique très utile pour guider les politiques publiques, en matière de campagnes de vaccination par exemple : quelle proportion de la population faut-il vacciner pour atteindre cette protection collective contre un pathogène ?
Il faut que le taux de personnes immunisées soit supérieur au taux d’immunité collective au moment où le pathogène est introduit dans la population pour que sa propagation soit fortement limitée et ne cause pas d’épidémie. La connaissance de ce taux peut également servir à évaluer le risque d’observer un reflux épidémique, c’est-à-dire une deuxième vague épidémique, selon le taux de personnes immunisées à la suite d’une première vague épidémique. En cas d’immunité non permanente au pathogène (comme cela semble être le cas pour le SARS-CoV-2), il faut également veiller à renouveler l’immunité de la population pour toujours rester au-dessus du taux d’immunité collective, afin d’éviter une nouvelle épidémie.
Attention cependant : l’immunité collective, en tant qu’indicateur statistique global, ne doit pas être utilisé au niveau individuel pour déterminer son propre risque d’être infecté en un lieu. Ce serait une erreur de raisonnement que de calculer un risque individuel à partir de statistiques agrégées.
Un monde simplifié pour comprendre l’immunité collective
Dans le modèle qui suit, nous disposons d’une population de 22 201 individus représentés par des carrés. Ces individus peuvent prendre 3 états distincts : sains, infectés (et donc contagieux) ou immunisés après avoir été infectés pendant un certain temps. Nous faisons l’hypothèse ici d’une immunité permanente : un même individu ne peut pas être réinfecté par le pathogène. Chaque individu a exactement 8 “voisins”. Ce ne sont pas vraiment des voisins au sens “les gens qui habitent à côté de chez moi”, mais plutôt des gens avec qui l’individu peut potentiellement être en contact au cours d’une journée (à titre de comparaison, une étude menée en 2008 donnait un nombre moyen de contacts quotidiens égal à 13,4). Dans notre modèle, les individus sains peuvent rencontrer chaque jour entre 0 et 8 de leurs voisins. Chaque rencontre avec une personne infectée comporte un risque de transmission du pathogène à l’individu sain.
Grâce à ce modèle, nous allons essayer de déterminer le taux d’immunité collective qui permettra d’éviter une épidémie dans notre population, à partir d’une seule personne infectée au départ.
La vidéo suivante montre la propagation du pathogène dans la population. Les personnes saines sont représentées en beige, les personnes infectées en bleu et les personnes guéries et immunisées en marron. La proportion de personnes immunisées initialement est de 0% dans la vidéo en haut à gauche, de 20% en haut à droite, de 40% en bas à gauche et de 50% en bas à droite.
Les graphes ci-dessous représentent l’évolution de la proportion d’individus dans chaque catégorie au cours de la simulation et correspondent aux vidéos juste au-dessus, dans le même ordre.
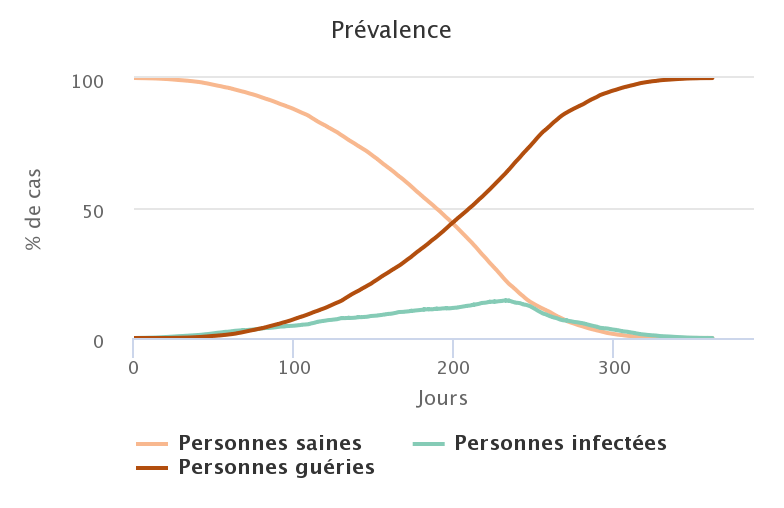
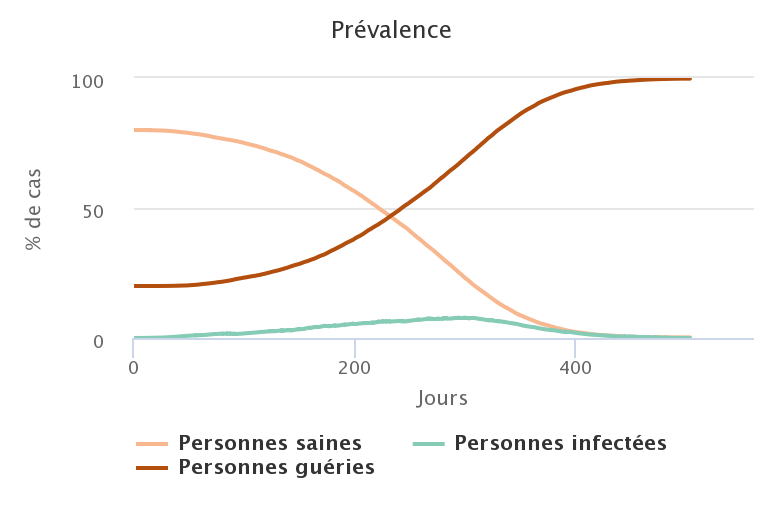
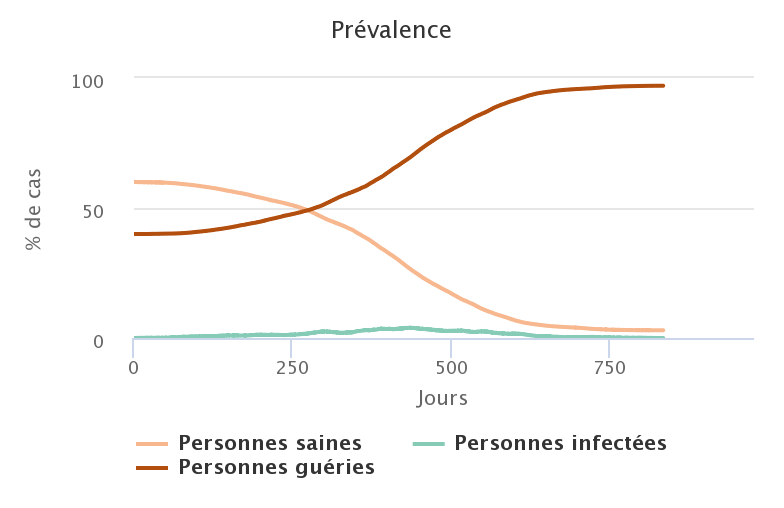
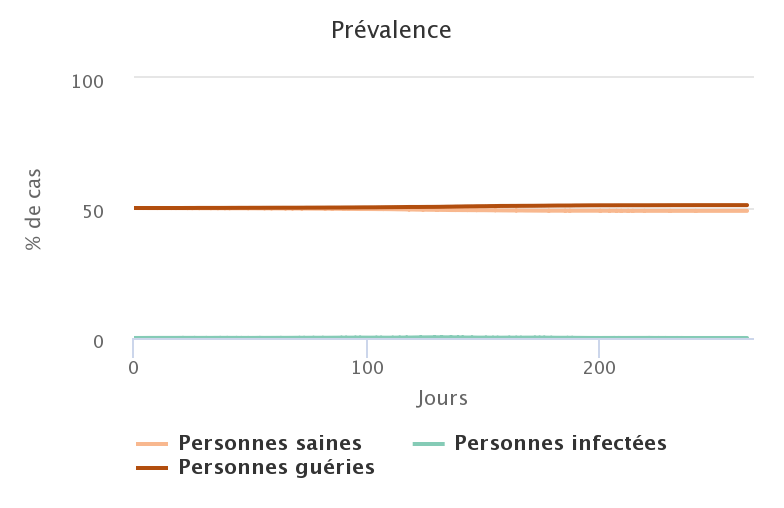
Sans surprise, plus le taux de personnes immunisées au départ est faible, plus le nombre de personnes ayant été infectées à la fin est grand.
| Proportion initiale d’immunisation |
Proportion finale d’infections |
|---|---|
| 0% | 99,97% |
| 20% | 99,69% |
| 40% | 95,03% |
| 50% | 2,2% |
Dans les trois premiers cas, on ne peut donc pas parler d’immunité collective, puisque l’immunité de 20 ou 40% de la population ne protège en rien les 80 ou 60% qui étaient sains au départ. En revanche, si on augmente à 50% la proportion de personnes immunisées, alors la diffusion du pathogène à partir d’un seul foyer d’infection initial ne parvient pas à se transformer en une épidémie : l’immunité collective a fonctionné et a permis de préserver une grande partie de la population initialement saine.
La recherche de ce gain marginal optimal, qui fait qu’une faible proportion supplémentaire de personnes immunisées (10% de plus) permet de réduire drastiquement le nombre de nouveaux cas d’infections, est le coeur de la recherche du taux d’immunité collective.
Si on reporte sur un graphique la proportion de personnes infectées à la fin d’une simulation (axe vertical) en fonction de différentes valeurs du taux de personnes immunisées à l’initialisation (axe horizontal), il est possible de déterminer graphiquement le taux d’immunité collective. Avec les paramètres employés, ici très favorables à la diffusion du pathogène, la proportion de personnes saines infectées à la fin de la simulation reste supérieure à 90% pour des taux d’immunisation jusqu’à 40%. À 45% de personnes immunisées initialement, on observe une légère diminution de la proportion finale de personnes infectées mais celle-ci reste toujours très élevée, à 77%. Il n’y a donc pas d’immunité de groupe dans ces cas là. Un effet de seuil significatif apparaît entre 45 et 50% d’immunisés : on voit une chute soudaine de la proportion de personnes infectées de 77% à 14% ! Ainsi, 5% de personnes immunisées supplémentaires au départ entraînent une diminution de plus de 60% des nouveaux cas enregistrés : l’immunité collective a fonctionné ! Et en poussant la proportion de personnes immunisées à 55%, on obtient seulement 1% de cas d’infections.
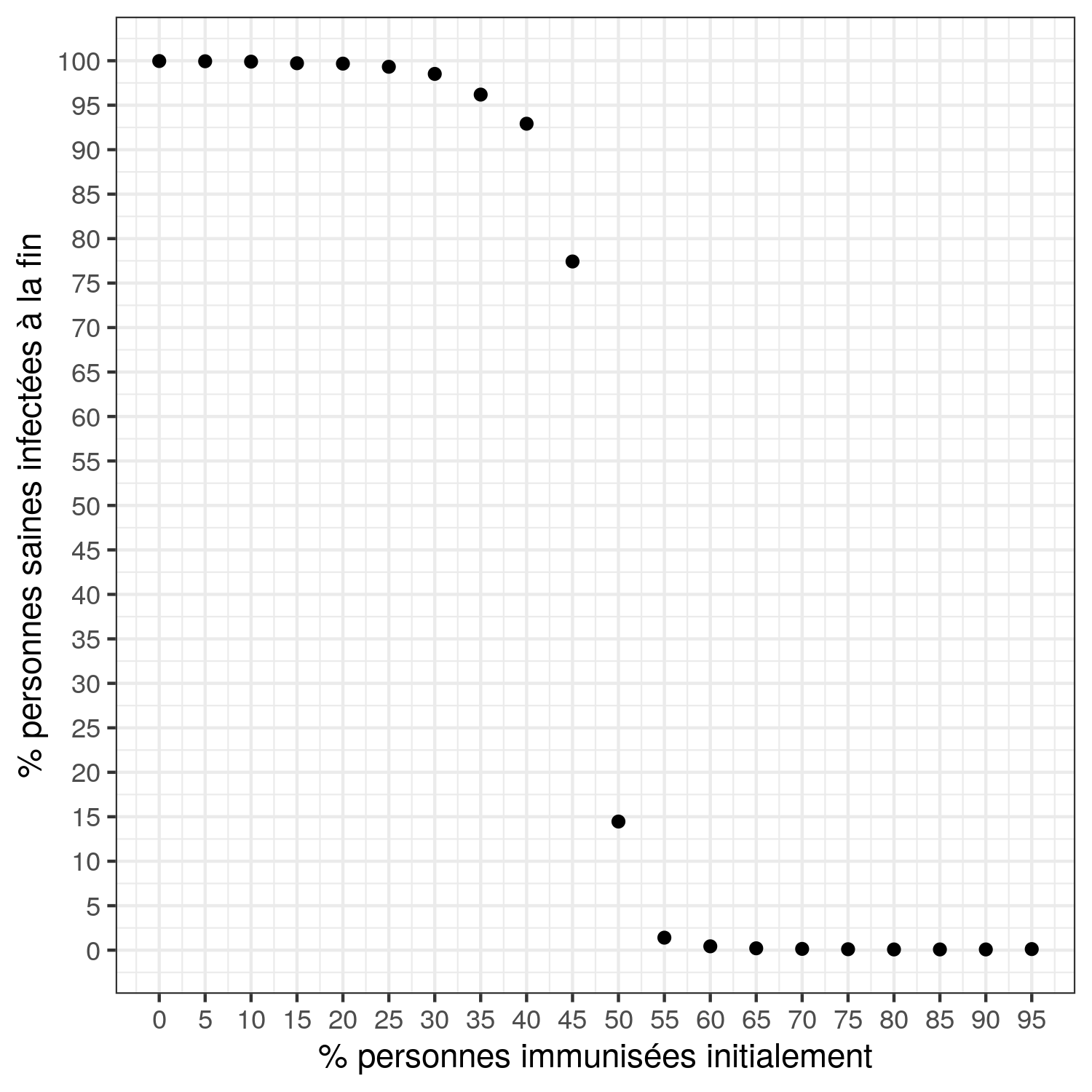
Le graphique ci-dessus présente les moyennes de la proportion finale de personnes saines obtenues lorsqu’on simule 1 000 fois le modèle pour une valeur donnée de la proportion initiale de personnes immunisées.
Le simulateur : à vous de jouer !
On commence par choisir la proportion de personnes immunisées initialement (entre 0 et 100%), puis on sélectionne la manière dont la population sera distribuée dans le monde avec le paramètre monde-spatialise? : soit aléatoirement (case décochée), soit spatialement structurée en Est/Ouest (case cochée). On définit les valeurs des paramètres que l’on souhaite tester, puis on initialise l’espace de simulation avec Initialiser.
À l’initialisation, un cas infecté est positionné aléatoirement dans la zone. À chaque fois que l’on clique sur initialisation, une nouvelle configuration spatiale apparaît. Le bouton Simuler lance la simulation. Des graphiques et des compteurs permettent de visualiser l’évolution de l’état de santé de la population. Selon le taux initial d’immunité de la population, le pathogène peut ne pas se propager ou s’arrêter dans sa progression. Vous pouvez alors décider d’introduire une ou plusieurs autres personnes infectées (valeur à déterminer par le curseur nb-nouvelles-infections) et valider ce choix (cliquer sur infecter de nouvelles personnes). Vous pouvez également choisir de créer de nouveaux cas en cours de simulation, pour représenter par exemple l’importation de nouveaux cas. Les sections qui suivent sont des exemples de scénarios qu’il est possible de tester avec ce simulateur. Vous pouvez par exemple observer commment varie le taux d’immunité collective lorsque le taux de transmission du pathogène ou la durée de contagiosité évoluent.
Attention : le modèle que nous vous présentons est stochastique. Cela signifie que certains des mécanismes représentés dans le modèle comportent des effets aléatoires. C’est le cas par exemple lors de l’initialisation du modèle : le choix des individus qui seront immunisés au départ est aléatoire, de même que le choix de la première personne infectée. C’est pourquoi lancer la simulation plusieurs fois avec les mêmes valeurs de paramètres donnera toujours des valeurs finales différentes, même si elles restent proches.
Si la fenêtre du simulateur est tronquée à l’affichage, il vous suffit d’effectuer un zoom arrière.
Modèle pour simuler l’immunité collective
Pour en savoir plus sur l’immunité collective en général et les pièges à éviter, nous vous invitons à cliquer sur le bouton “Aller plus loin” ci-dessous. Pour plus d’informations sur l’immunité collective dans le cadre de l’épidémie actuelle de COVID-19, un autre post est en préparation !
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.