L’application mobile StopCovid, destinée à briser la chaîne de transmission d’un malade en identifiant ses contacts rapprochés, fait couler beaucoup d’encre. Au-delà des questionnements légitimes liés à la faisabilité technique et opérationnelle d’un tel dispositif, ceux relatifs à ses possibles effets pervers ainsi qu’à son efficacité espérée dans la lutte contre la COVID-19 sont tout aussi nombreux.

Pourtant l’idée de départ est aussi simple que séduisante : identifier et casser rapidement les chaînes de transmission du virus. La manière traditionnelle d’atteindre ce résultat est un travail d’enquête. Un malade symptomatique est signalé à l’Assurance Maladie, qui lance alors une enquête pour essayer de retrouver les contacts que cette personne a eu au cours des derniers jours, dans le but de les prévenir et de leur proposer un test avant qu’eux-mêmes ne contaminent d’autres gens.

Une application mobile peut aider à accomplir ce travail d’enquête. Voyons ceci plus en détail en imaginant un scénario idéal :
Roger, 55 ans, a installé l’application sur son téléphone. Il se réveille un beau matin avec des symptômes évoquant la COVID-19. Il consulte son médecin, qui lui prescrit un test PCR. Celui-ci est réalisé rapidement. Les résultats tombent immédiatement : Roger est testé positif et a donc contracté la COVID-19. Roger s’isole à son domicile et décide de prévenir ses contacts de son changement de statut épidémique. L’application émet alors un signal qui est automatiquement transmis à toutes les personnes possédant l’application qu’il a pu croiser - à une distance et pendant une durée compatibles avec une transmission du virus - les quelques jours précédant la mise œuvre du test, c’est-à-dire pendant la phase d’incubation de la maladie. Ses contacts effectuent à leur tour un test et si le résultat de celui-ci est positif, ils préviennent également leurs contacts - qui préviendront à leur tour leurs contacts et ainsi de suite - puis se placent immédiatement en isolement pendant au moins deux semaines.

Ainsi, en quelques heures, un porteur identifié et plusieurs personnes à risque sont retirés du “jeu”, affaiblissant de ce fait la chaîne de transmission du virus.

Ce récit a des allures de science-fiction, surtout si on le compare aux modalités de lutte contre l’épidémie mises en oeuvre en France depuis le début de cette crise, davantage fondées sur des stratégies élémentaires (gestes barrières, distanciation physique, confinement) et de gestion de la pénurie (en masques et en moyens de dépistage notamment).
En supposant que le protocole “Roger” fonctionne parfaitement (nous définirons plus loin ce que nous entendons par là), la question à laquelle nous chercherons plus précisément à répondre est la suivante : quel serait son impact sur l’épidémie en terme de maîtrise du pic épidémique d’une part et limitation de la population à isoler d’autre part ?

Ce que la littérature scientifique nous apprend

Deux études scientifiques publiées pendant le confinement sont assez pessimistes. En effet, compte tenu du R0 que l’on suspecte en Europe (de l’ordre de 2,5), l’épidémie pourrait être maîtrisée (c’est-à-dire que le R0 serait ramené à une valeur inférieure à 1) grâce au déploiement d’une telle application selon les modalités suivantes : un taux de couverture de l’ordre de 100 % et un respect sans faille des consignes d’isolement. Une seconde étude prédit quant à elle que ce résultat pourrait être atteint à la condition supplémentaire que le déploiement se fasse aux premiers signes de l’épidémie et vraisemblablement en accompagnement d’autres mesures de prevention et de contrôle.

Comment expliquer ces résultats alors que, depuis le début de l’épidémie, le succès de Singapour dans la gestion de la crise est régulièrement mis en avant, avec un taux de couverture pour son application mobile de l’ordre de seulement 20% (contre 75% visés par les autorités) ?

Précisons d’abord qu’il est très difficile d’isoler l’effet propre d’une mesure spécifique lorsque c‘est un ensemble de mesures complémentaires qui sont mises en place. Ainsi, Singapour s’est distinguée par sa mobilisation très rapide dès le début de l’épidémie et sa capacité à identifier les premiers cas à l’origine de la propagation du virus sur son territoire. Dans la foulée, le port du masque généralisé, les dépistages nombreux, l’adhésion massive de la population aux gestes barrières et aux règles de distanciation sociale ont sans doute joué un rôle important. Il est donc très difficile de distinguer l’impact spécifique des outils numériques dans ce dispositif très complet.

Rappelons enfin que Singapour a fini par mettre en place un confinement partiel le 7 avril alors même que l’épidémie y semblait jusqu’ici plutôt maîtrisée (un état des lieux très complet de la situation à Singapour est accessible ici).

Le modèle développé par CoVprehension

Afin de produire une alternative indépendante aux modèles produits dans les deux articles cités plus haut, nous avons développé notre propre modèle à partir des éléments de base du modèle de confinement de la Q6.

Dans ce nouveau modèle, les journées sont ainsi découpées en quatre tranches de 6 heures. Les trois premières tranches sont occupées par des déplacements et des rencontres (en moyenne 10 par jour et par personne). La plupart des déplacements se font à proximité du domicile mais 20% d’entre eux se font à plus longue distance. La dernière tranche de la journée s’effectue au domicile, qui est partagé par trois personnes en moyenne. Au total, 2000 personnes occupent ce petit territoire virtuel.

Par ailleurs, nous introduisons également une phase d’incubation (E pour Exposé) et deux catégories d’infection possibles : les symptomatiques et les asymptomatiques, ces dernières étant plus difficiles à identifier par simple diagnostic médical en raison de l’absence de symptômes. Il s’agit donc maintenant d’un modèle SEIR, dont nous décrivons les différents changements d’état sous forme graphique (figure 1).

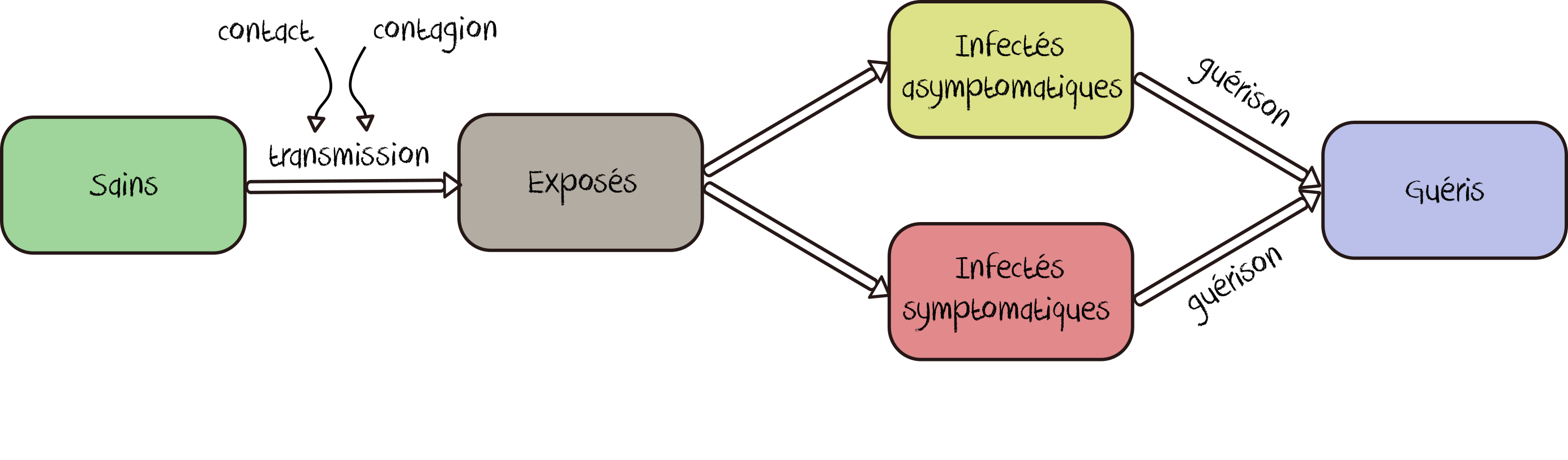
Figure 1 : représentation graphique du cheminement épidémique des individus dans le modèle SEIR développé

À l’initialisation, tous les individus sont sains. On injecte alors un petit nombre d’individus infectés (paramètre Nombre-de-cas-au-départ) dans cette population initiale et on simule la propagation du virus à partir des comportements des individus modélisés. Les changements d’état s’opèrent de la manière suivante et reprennent les valeurs de référence fixées par l’Institut Pasteur :

Sain → Exposé : un individu sain deviendra exposé, au contact d’un individu infecté, selon une probabilité qui dépend de la valeur du R0 choisie et de la catégorie à laquelle appartient cet individu infecté (cf point suivant). La formule retenue pour calculer cette probabilité est la suivante : P(S→ E) = 1/R0 x c x d avec c le nombre de contacts moyens par jours (fixé à 10 environ, comme dans la Question 10) et d la durée de la période contagieuse.
Exposé → Infecté : un individu restera dans l’état exposé pendant sa période d’incubation (fixée ici à 5 jours), au cours de laquelle il deviendra progressivement contagieux, jusqu’à devenir Infecté asymptomatique (3 chances sur 10) ou Infecté symptomatique (7 chances sur 10). La contagiosité d’un individu symptomatique est estimée à partir du R0 (cf point précédent) et est considérée comme étant deux fois supérieure à celle d’un individu asymptomatique.
Infecté → Guéri : au bout de 14 jours, un individu infecté est considéré comme guéri et non contagieux dans le modèle.

Sur cette base, quatre scénarios distincts sont proposés (paramètre SCENARIO), dans une perspective comparative. Nous en présentons ici les grandes lignes, leurs détails précis seront exposés par la suite :

S1 “Laisser-faire” : on ne fait rien, l’épidémie suit son cours sans aucune interférence ;
S2 “Isolement simple” : on identifie les porteurs symptomatiques (test) et on les isole avec leur famille (entendue ici comme les personnes qui partagent le même toit) ;
S3 “Traçage et isolement systématique” : les porteurs symptomatiques sont systématiquement testés et ceux qui sont positifs sont isolés tandis que leurs contacts sont isolés sans être testés ;
S4 “Traçage et isolement sélectif” : les porteurs symptomatiques sont systématiquement testés et ceux qui sont positifs sont isolés, tandis que leurs contacts (et leurs contacts) sont testés puis isolés si le test est positif.

Détaillons le scénario Traçage et isolement sélectif (c’est notre scénario “Roger”, et le plus proche de l’utilisation prévue de l’app française StopCovid), qui cumule la plupart des caractéristiques des autres scénarios .

Dans ce scénario, un certain nombre d’individus choisis au hasard sont équipés de l’application mobile, en fonction du paramètre Taux-de-couverture-de-l’application-de-traçage fixé par l’utilisateur. Lorsqu’un individu équipé devient infecté symptomatique, il est alors soumis à un test PCR (dans un délai fixé par le paramètre Temps-d’attente-pour-la-réalisation-du-test), dont la capacité à identifier l’infection (sa sensibilité) est définie par le paramètre Probabilité-que-le-test-soit-efficace. Avec une valeur de 1, ce paramètre indique que le test est positif pour toutes les personnes infectées testées. Si sa valeur est fixée à 0,5 alors le test sera positif pour seulement la moitié des personnes infectées testées.

Par ailleurs, dans ce modèle, le test n’est jamais positif en testant une personne qui n’est pas infectée : il est parfaitement spécifique.

Si l’individu est testé positif, il active alors son application et se met en isolement (avec une rigueur dans le respect de son isolement qui dépend du paramètre Probabilité-de-respect-isolement), jusqu’à la disparition des symptômes. À partir de ce moment, les personnes porteuses de l’application de traçage qu’il a croisées au cours des n jours précédant son dépistage (la valeur de n dépendant du paramètre Profondeur-pour-l’identification-des-contacts), sont testées systématiquement, puis, si elles sont testées positives, se mettent elles-mêmes en isolement et alertent leurs propres contacts. Attention, on a pu lire une confusion à ce sujet : quand on parle de contacts dans le contexte de cette application, on parle d’identifiants cryptés dans l’application des contacts physiques enregistrés, et absolument pas des contacts dans le répertoire du téléphone !

Petite note sur le R0

Le R0, ou nombre de reproduction de base, est un indicateur global de la dynamique épidémique. De manière intuitive on peut le voir comme un indicateur du nombre de personnes saines qu’une personne contagieuse contaminera, en moyenne, au début de l’épidémie. Au cours de l’épidémie, le nombre de reproduction évoluera, on parlera de R(t). Si R0, qui est donc aussi R(0), représente la “férocité” intrinsèque de l’épidémie sur un territoire donné, R(t) représentera l’évolution de la contagion au cours du temps et en fonction des mesures appliquées.

Si la valeur de R au cours du temps devient inférieure à 1, l’épidémie va s’éteindre d’elle même. Si R reste supérieur à 1, alors l’épidémie continuera à se développer.

Vous pouvez tester l’impact du R0 en faisant varier la valeur du paramètre R0-fixé à l’initialisation.

À noter: avec un R0-fixé égal à deux, vous pouvez éventuellement obtenir des situations dans lesquelles l’épidémie s’éteint rapidement, en raison du caractère discret et stochastique du modèle. C’est possible, mais peu probable.

Attention, R0 est une composition de 3 processus couplés : le taux de contacts dans la population, la probabilité de transmission du virus à chaque contact et la durée de la phase contagieuse de la maladie développée. Par ailleurs, comme tout indicateur global, il ne rend pas compte des situations locales, qui peuvent être très différenciées. Il doit donc être manipulé avec précaution.

Son utilisation dans ce modèle permet de caractériser des dynamiques épidémiques types. À titre d’exemple, le R(t) en France au moment de la mise en place de la période de confinement (17 mars 2020) était estimé à une valeur comprise entre 2,5 et 3,5. Après plusieurs semaines de confinement, R(t) était descendu à une valeur inférieure à 1, grâce à la mise en place du confinement mais aussi de l’adoption des gestes barrières et d’une distanciation physique appliquée de manière relativement généralisée. En ce sens, la dynamique épidémique sous-jacente observée à ce moment là peut être considérée comme artificielle et ne reflète donc plus la dynamique initiale, telle qu’elle a été modélisée ici.

Testez vous-même ces différentes stratégies en les simulant

Le simulateur vous permet de tester ces différentes stratégies, pour un nombre de personnes initialement infectées et un R0 fixés. Si la fenêtre du simulateur est tronquée à l’affichage, il vous suffit d’effectuer un zoom arrière

Simuler l’impact de mesures d’isolement avec ou sans traçage des contacts

Alors, le traçage ça marche ou pas ?

Afin de comparer les performances des différents scénarios, nous avons simplifié le problème en posant les conditions initiales communes suivantes :

la taille de la population est de 2000 personnes ;
80% des déplacements se font à proximité du domicile et 20% d’entre eux se font à plus longue distance ;
le nombre de personnes contagieuses au départ est égal à 10, soit 0,5% de la population ;
le R0 fixé à l’initialisation prend trois valeurs différentes : 1, 2 et 3 ;
la durée de la phase d’incubation est de 5 jours ;
la durée de la phase contagieuse après la phase d’incubation est fixée à 14 jours ;
la proportion de porteurs asymptomatiques est fixée à 30% ;
les tests sont disponibles en moins de 6h ;
les tests sont fiables à 95% ;
les personnes testées positives préviennent systématiquement leurs contacts via l’appli ;
les personnes testées positives se placent systématiquement en isolement pendant 21 jours et le respectent scrupuleusement ;
chaque simulation est répétée 100 fois, afin de prendre en compte le caractère stochastique du modèle, i.e. la présence d’aléa.

Le graphique suivant compare les performances des quatre scénarios pour un indicateur d’activité épidémique : le pic de l’épidémie (en proportion de la population concernée). Pour chaque scénario, les résultats sont représentés sous forme de boîtes à moustaches : 25% des simulations donnent des valeurs supérieures à la limite supérieure de la boîte, 25% donnent des valeurs inférieures à la limite inférieure de la boîte et la ligne à l’intérieur de la boîte donne la médiane (i.e. 50% des valeurs lui sont supérieures et 50% inférieures). On a également distingué les trois valeurs de R0 fixées à l’initialisation. Dans notre cas, plus une boîte (et surtout la valeur médiane) est proche de zéro, plus le pic épidémique correspondant est petit et donc le dispositif du scénario correspondant efficace. Par ailleurs, plus la boîte est haute et plus les résultats sont variables. Enfin, les points sont des valeurs extrêmes (outliers), très éloignés de la distribution statistique à l’intérieur de la boîte et de ses moustaches.

Performance des 4 scénarios en terme de maîtrise du pic de l’épidémie

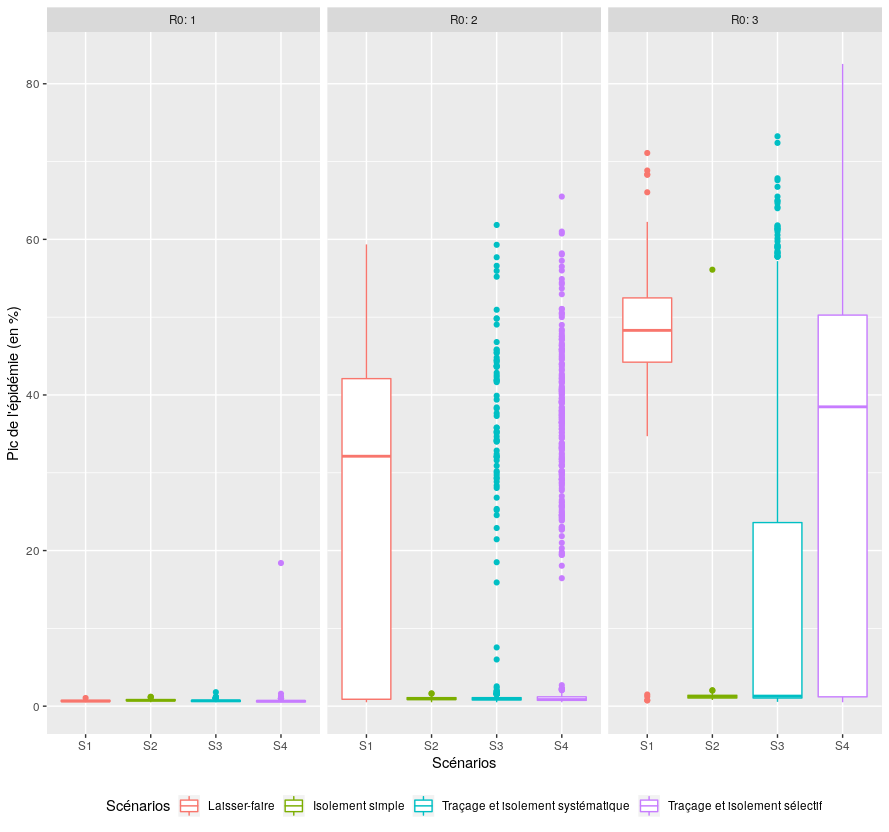
Figure 2 : Comparaison des performances des quatre scénarios pour l’indicateur “Pic de l’épidémie”.

Lorsque R0 est égal à un, aucun des trois scénarios de contrôle ne fait mieux - dans le modèle -, que le scénario “Laisser-faire”. Les dispositifs de traçage des contacts réalisent toutefois de bonnes performances lorsque R0 est égal à deux, sans pour autant faire mieux (de manière statistiquement significative) que le scénario basique de confinement des porteurs symptomatiques (S2). En revanche, seul ce dernier scénario à même de contenir le pic épidémique même pour un R0 égal à trois. Regardons maintenant ce qu’il en est de la population confinée pendant l’épidémie : après tout, l’une des plus-values de l’application StopCovid est censée être sa capacité à mettre en place un isolement très sélectif, en ciblant les personnes contagieuses.

Performance des scénarios S2, S3 et S4 en terme de limitation de la population isolée

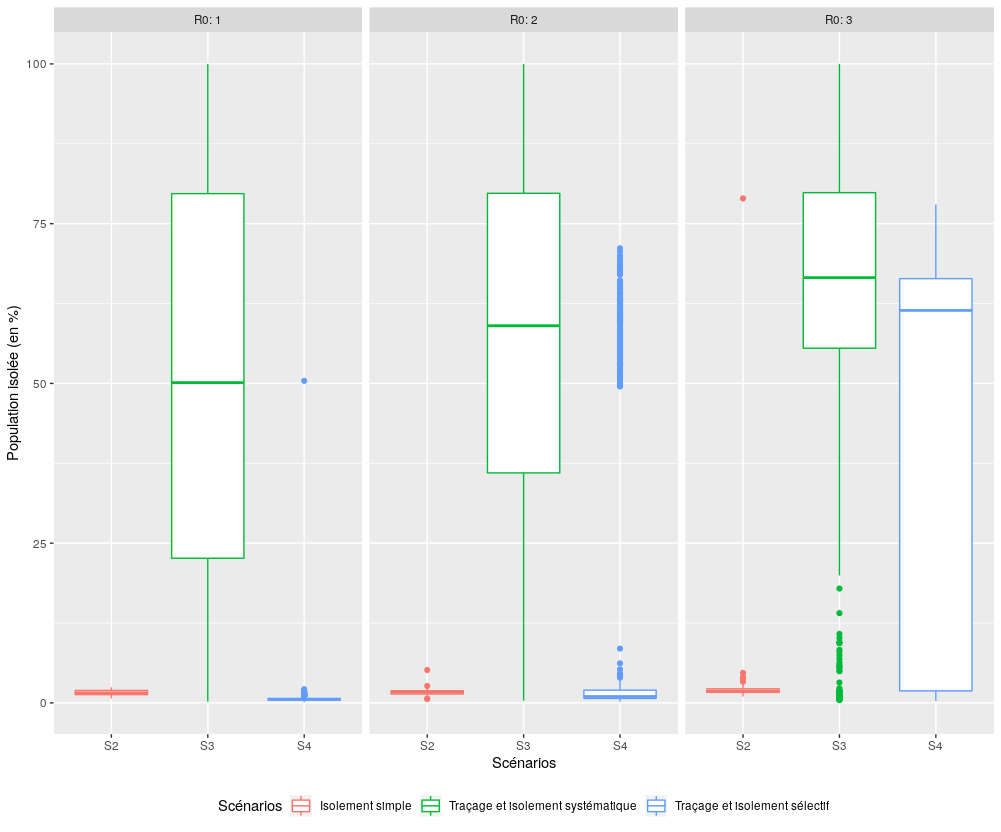Figure 3 : Comparaison des performances des trois scénarios impliquant un isolement (S2, S3, S4), pour l’indicateur “Proportion de la population isolée pendant l’épidémie”.

Le scénario S4 obtient (suivi de près par le scénario S2) les meilleurs résultats pour un R0 inférieur ou égal à deux. En revanche, lorsque R0 est égal à trois, seul le scénario S2 est à même de limiter la population isolée.

Performance des scénarios S2, S3 et S4 en terme de capacité à ne pas isoler inutilement la population non contagieuse

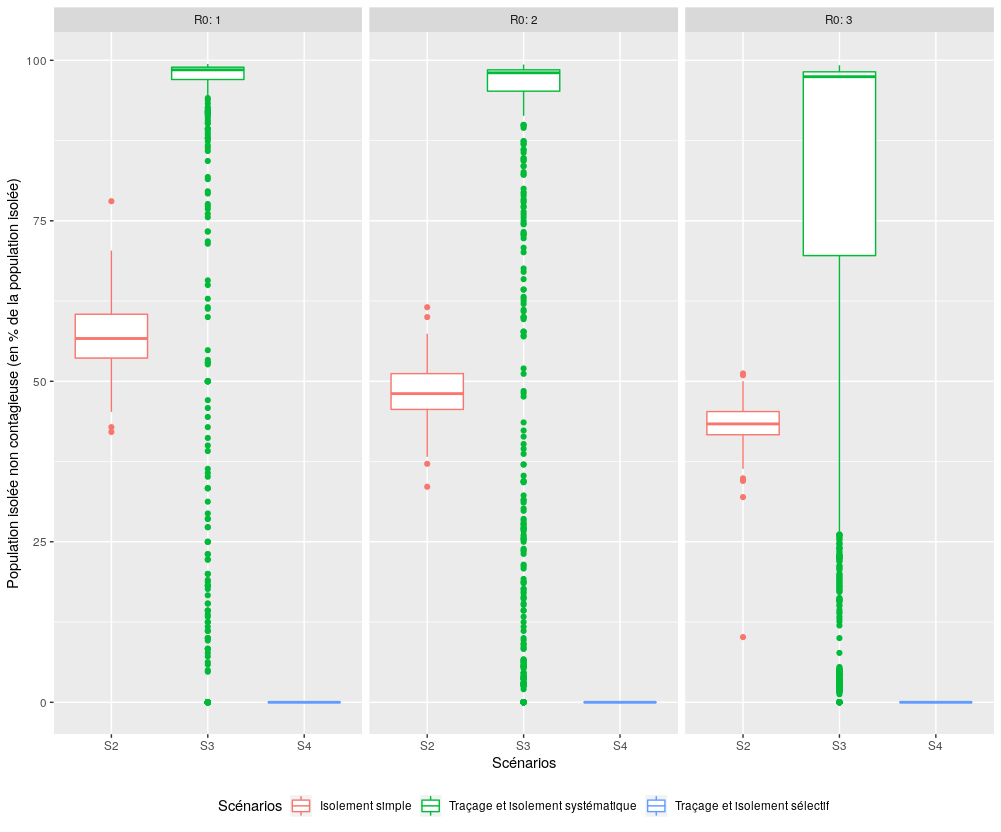
Figure 4 : Comparaison des performances des trois scénarios impliquant un isolement (S2, S3, S4), pour l’indicateur “Proportion de la population non contagieuse isolée pendant l’épidémie”.

Le scénario S4 montre ici tout son intérêt, puisqu’il permet de n’isoler que des individus contagieux, grâce au traçage des contacts et le recours systématique à des tests. Pour un R0 inférieur ou égal à deux, le scénario S4 est donc bien le plus performant en terme d’isolement. Ce résultat doit toutefois être ramené à la très bonne performance du scénario S2, qui limite globalement tout aussi bien la population isolée, même s’il est moins efficace en terme de tri entre personnes contagieuses et non contagieuses. Essayons maintenant d’affiner cette première analyse en nous concentrant sur les deux scénarios S3 “Traçage et isolement systématique” et S4 “Traçage et isolement sélectif”, de manière à comparer plus précisément leurs performances pour des taux de couverture qui varient de 10% à 100% de la population.

Performance des scénarios avec traçage (S3, S4) en terme de maîtrise du pic de l’épidémie

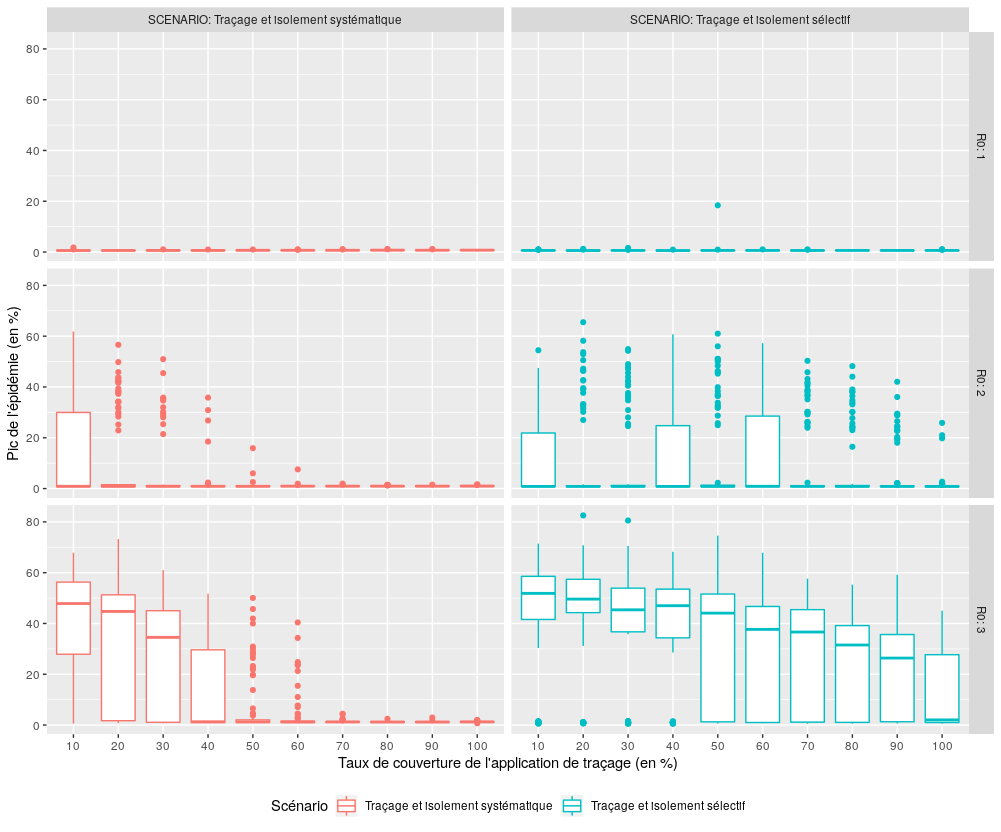
Figure 5 : Comparaison des performances des deux scénarios avec traçage des contacts (S3 et S4) pour l’indicateur “Pic de l’épidémie”.

Pour R0 inférieur ou égal à deux, le taux de couverture ne joue aucun rôle dans la maîtrise du pic épidémique (les médianes sont proches de zéro). Lorsque R0 est égal à trois, le scénario S3 parvient à maîtriser l’intensité du pic épidémique lorsque son taux de couverture approche 50% de la population (contre 100% pour le scénario S4).

Performance des scénarios avec traçage (S3, S4) en terme de limitation de la population isolée

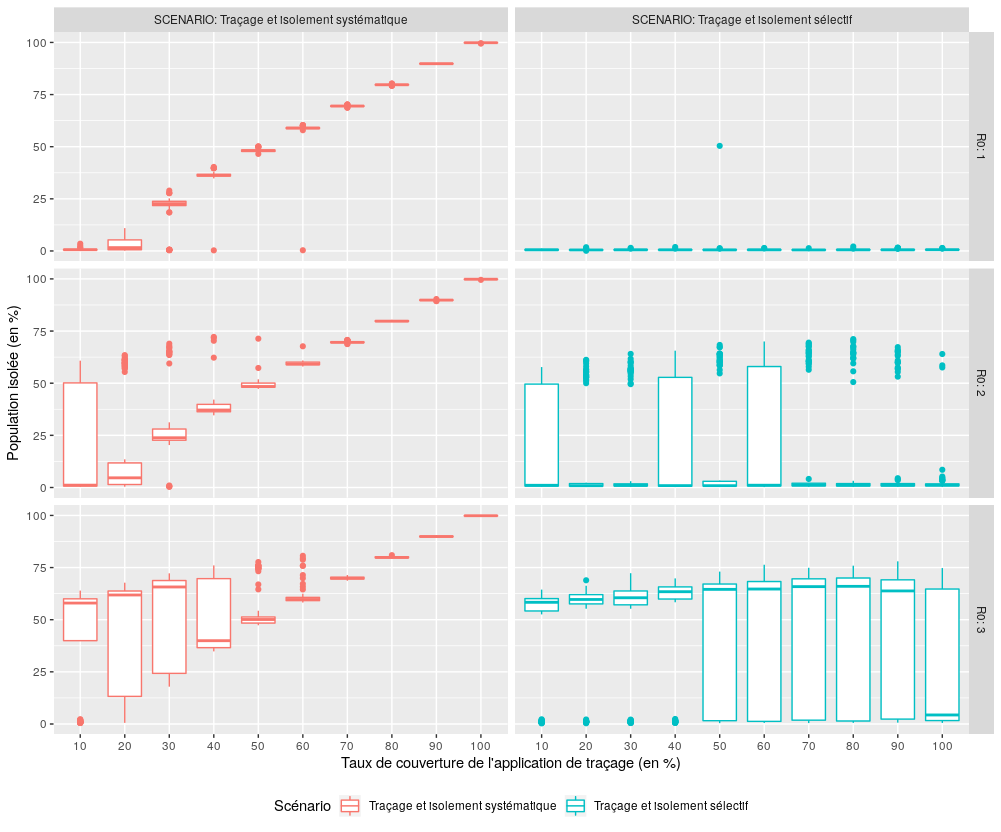
Figure 6 : Comparaison des performances des scénarios S3 et S4 pour l’indicateur “Population isolée”.

Les deux scénarios se comportent de manière significativement différente : le scénario S3 “Traçage et isolement systématique” isole une proportion croissante de la population à mesure que son taux de couverture augmente, tandis que le scénario S4 “Traçage et isolement sélectif” parvient à maintenir à un niveau relativement bas et constant la proportion de population isolée, quel que soit le taux de couverture, pour un R0 inférieur à 2.

Performance des scénarios avec traçage (S3, S4) en terme de ciblage de la population isolée

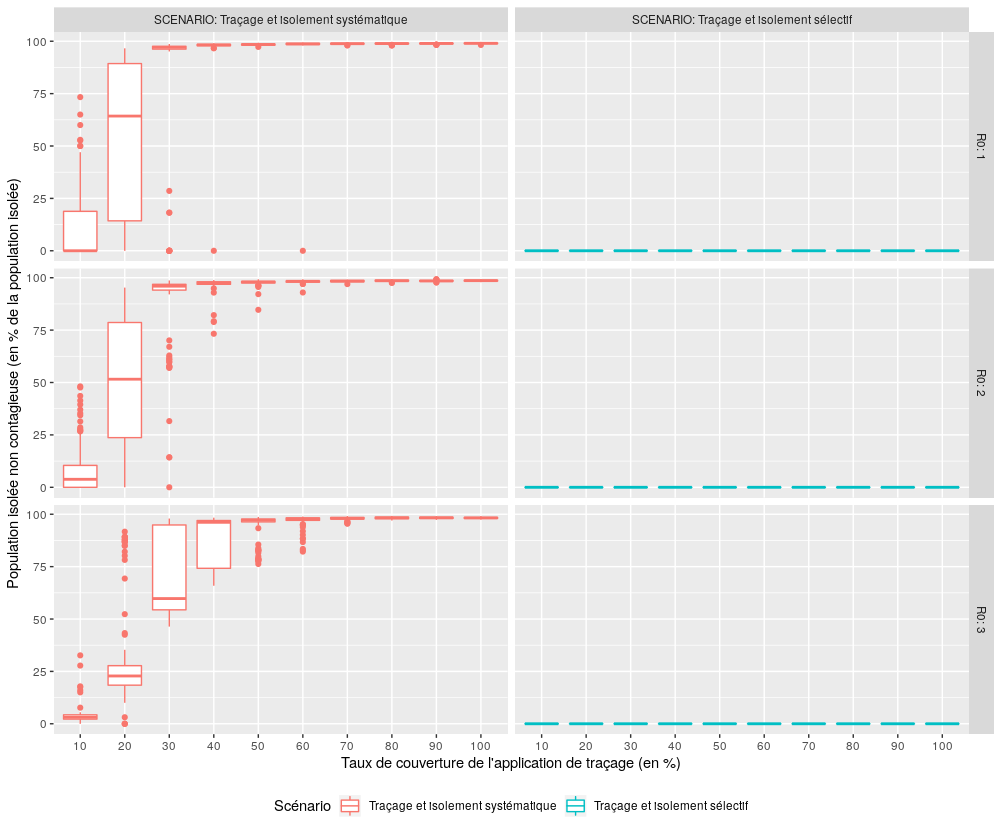
Figure 7 : Comparaison des performances des scénarios S3 et S4 pour l’indicateur “Population non contagieuse isolée”.

On voit clairement ici l’intérêt du scénario S4 “Traçage et isolement sélectif” par rapport au scénario S3 “Traçage et isolement systématique”, qui isole une grande partie de la population dès que 30% d’entre elle est équipée de l’application de traçage. On voit également sa pertinence par rapport au scénario S2 “isolement simple”, qui conduit à isoler une proportion certes très réduite de la population (en médiane autour de 1% de la population pour les trois valeurs testées de R0) mais pour moitié constituée de personnes non contagieuses (ie saines ou guéries). Par ailleurs et de manière logique, la capacité des applications de traçage à détecter par traçage les personnes contagieuses dépend directement du taux de couverture : plus celui-ci est faible, plus le travail de détection est réalisé par l’identification des cas symptomatiques.

Performance des scénarios avec traçage (S3, S4) en terme d’identification et d’isolement des personnes contagieuses

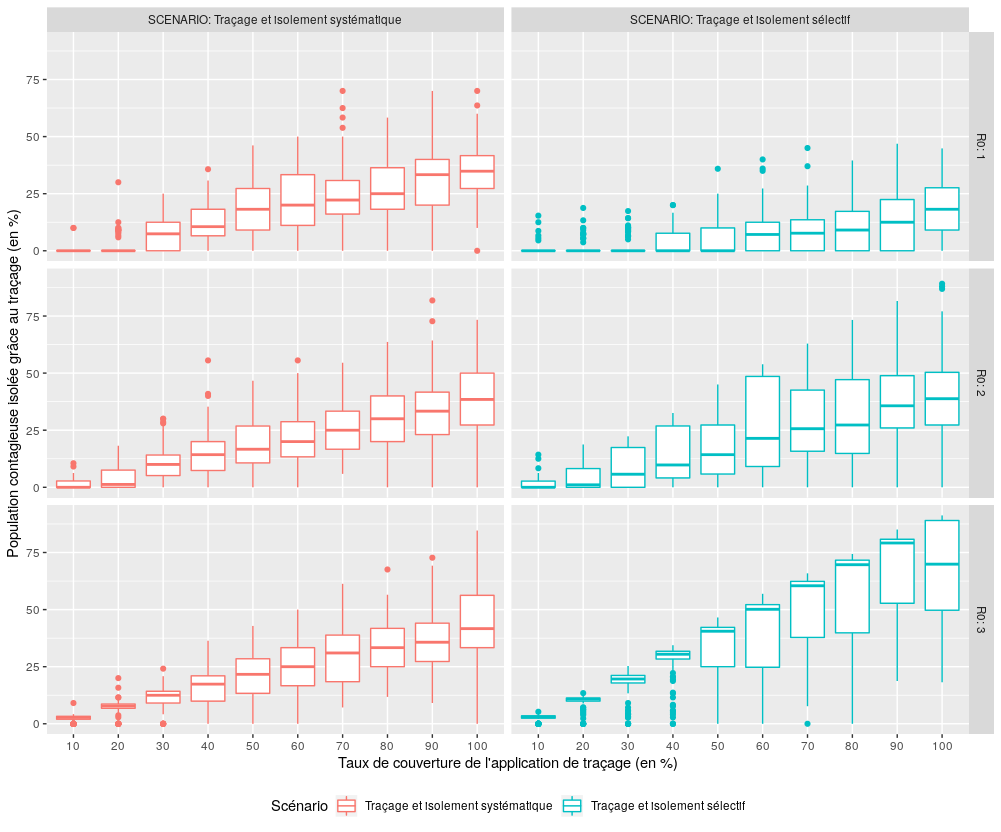
Figure 8 : Comparaison des performances des scénarios S3 et S4 pour l’indicateur “Parmi la population contagieuse confinée au cours de la simulation, quelle proportion a été isolée grâce au traçage des contacts par l’application ?”.

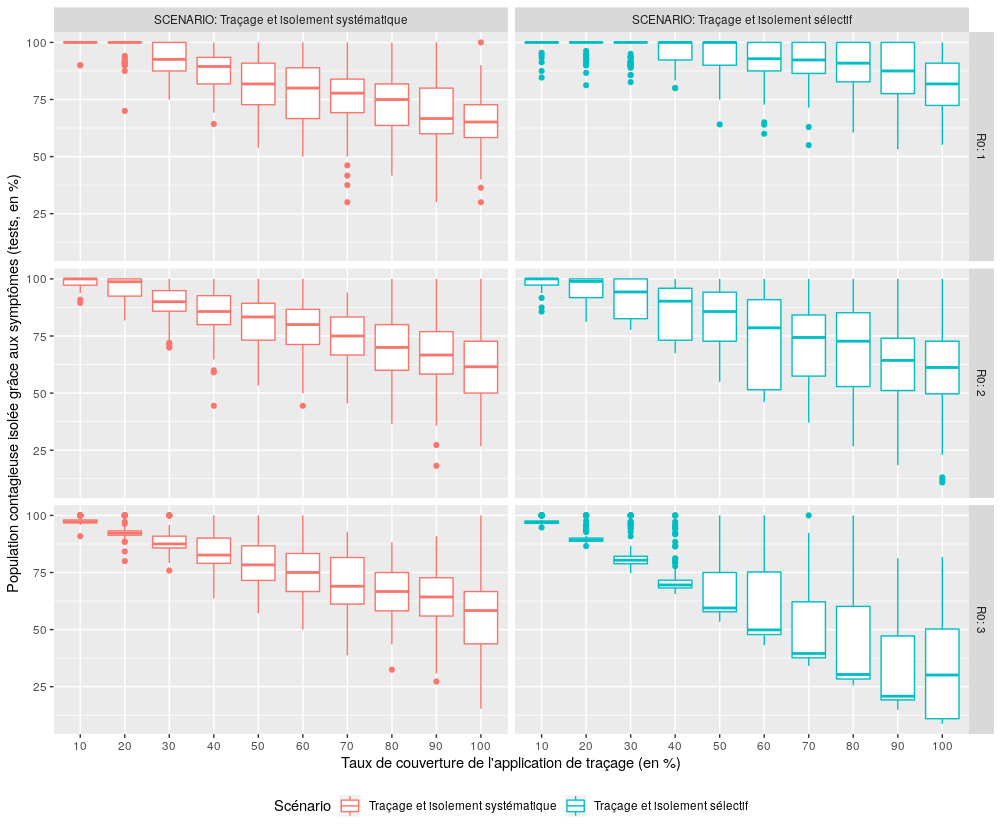
Figure 9 : Comparaison des performances des scénarios S3 et S4 pour l’indicateur “Parmi la population contagieuse confinée au cours de la simulation, quelle proportion a été isolée grâce aux symptômes (tests) (vs par l’application) ?”.

Contrairement à ce que l’on on aurait pu imaginer, l’identification initiale des porteurs symptomatiques reste un élément central du dispositif (en médiane et pour R0 inférieur ou égal à deux, plus de 60% des cas identifiés le sont grâce aux symptômes) et l’augmentation du taux de couverture des applications de traçage n’entraîne qu’une progression lente de la part de cette population identifiée grâce au traçage. Celle-ci ne dépasse jamais 40% des cas identifiés, sauf lorsque R0 est égal à deux et que le taux de couverture de l’application de traçage S4 est supérieur ou égal à 60%.

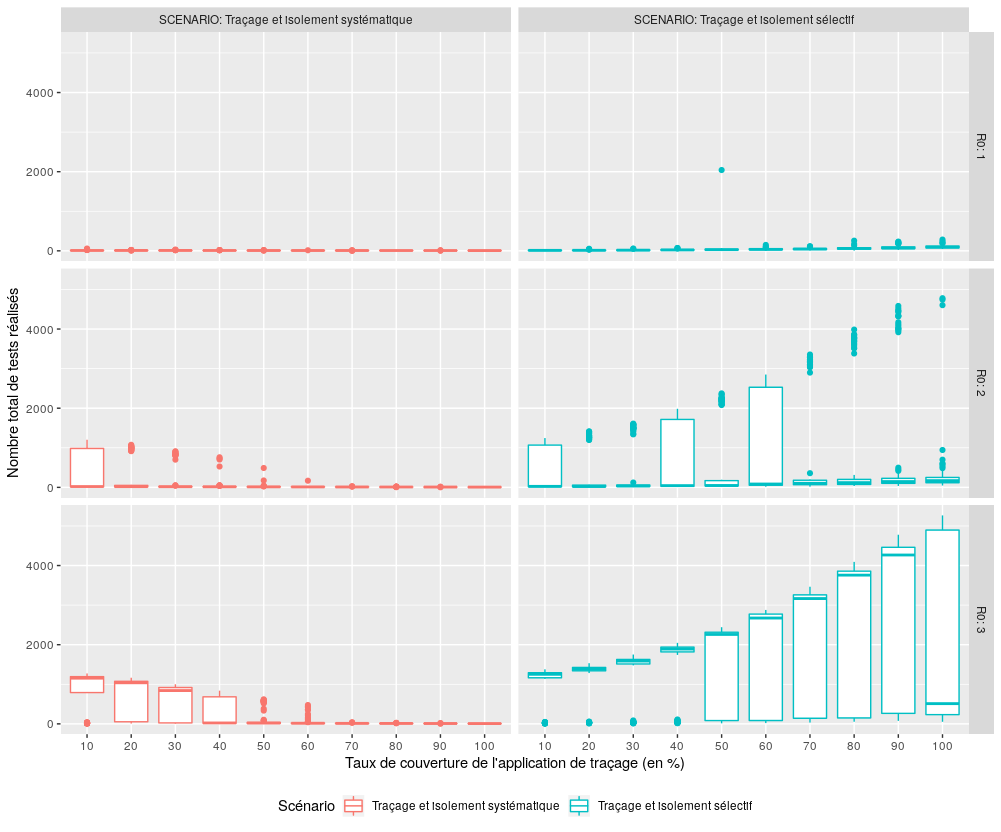
Figure 10 : Comparaison des performances des scénarios S3 et S4 pour l’indicateur “Nombre total de tests réalisés”. Le scénario S4 est par définition gourmand en tests, mais pas autant qu’on aurait pu s’y attendre. Pour un R0 égal à deux, ce nombre reste faible (moins de 5% de la population totale en médiane), même s’il croît avec le taux de couverture de l’application. En revanche, lorsque le R0 est égal à trois, le nombre de tests augmente rapidement pour dépasser la taille de la population lorsque le taux de couverture est égal à 50%, ce qui s’explique par le fait que certaines personnes sont testées plusieurs fois au cours de l’épidémie.

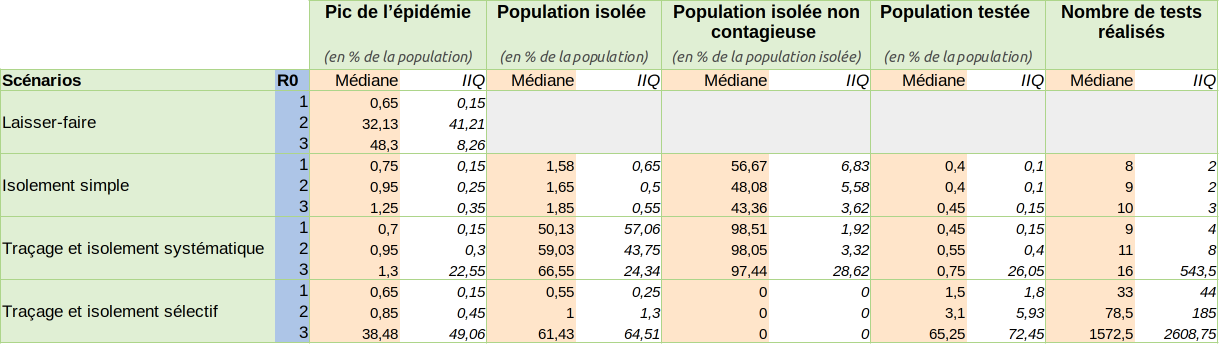
Figure 11 : Comparaison finale des performances des quatre scénarios S1, S2, S3 et S4 pour les principaux indicateurs retenus. Les valeurs sont estimées sur cent réplications de chaque simulation. L’intervalle inter-quartiles (IIQ) correspond à la hauteur de la boîte à moustache et donne donc une indication de la variabilité des résultats autour de la médiane.

Au final, lorsque R0 est égal à deux, le scénario S4 “Traçage et isolement sélectif” obtient les mêmes résultats en terme de maîtrise du pic épidémique que le scénario S2 “Isolement simple” (la différence observée de médiane n’est pas statistiquement significative, d’après le test non paramétrique U de Mann-Whitney. En revanche, la différence observée de l’ordre de 0.65% (1,65% pour S2 contre 1% pour S4) en terme de population isolée médiane, entre les scénarios S2 et S4, est bien statistiquement significative. Cette différence doit dès lors être évaluée dans le contexte d’une population bien plus nombreuse que nos 2000 individus modélisés. Ainsi, ramenée à une population de 67 millions et toutes choses égales par ailleurs, le scénario S4 conduirait - dans le cas d’un R0 égal à deux - à isoler 670 000 personnes, toutes contagieuses, dans le modèle là où le scénario S2 en isolerait plus d’un million (1 105 500) dont près de la moitié (530 640) non contagieuses. Et ceci, même avec un taux de couverture faible (inférieur à 20%). Ce succès ne vaut toutefois que pour R0 égal à deux, la proportion de population isolée explosant littéralement dans le scénario S4 lorsque R0 passe à trois, contrairement au scénario S2 qui affiche une grande robustesse dans ses performances.

Conclusion : traçage ou pas traçage ?

Rappelons d’abord que nous nous sommes placés volontairement dans un cadre idéal, et donc peu réaliste, mais qui présente l’avantage de fixer un cadre de référence ainsi que des objectifs à atteindre en terme de lutte contre l’épidémie :

les tests PCR sont disponibles en nombre et en moins de 6h ;
les tests PCR sont fiables à 95% ;
les personnes testées positives préviennent systématiquement leurs contacts via l’appli ;
les personnes pour lesquelles l’isolement est conseillé respectent scrupuleusement cette consigne.

Précisons ensuite que nos conclusions ne sont valables que par rapport au modèle épidémique développé. Enfin, soulignons à nouveau que les valeurs de R0 utilisées doivent être interprétées avec précaution. Ainsi, la dynamique post-confinement de l’épidémie en France, dont le R0 est estimé à 0.6 ou 0.7, ne peut pas directement être assimilée à une même valeur de un pour le paramètre RO-fixé de notre modèle. En effet, la situation post-confinement française se caractérise par plusieurs semaines de confinement, ainsi que par l’adoption de gestes barrières et d’une distanciation physique relativement généralisée. En ce sens, la dynamique épidémique sous-jacente est artificielle et ne reflète pas la dynamique initiale, qui est celle modélisée ici.

Que pouvons-nous conclure de cet exercice de modélisation au final ?

Tout d’abord, les deux dispositifs de traçage des contacts testés par simulation (les scénarios 3 et 4) ne produisent pas de miracles lorsque la dynamique épidémique est trop faible (R0 égal à un) ou trop forte (R0 égal à trois). Dans le premier cas (R0 égal à un), l’épidémie s’arrête d’elle même dans le modèle et aucun scénario interventionniste ne fait mieux que le scénario de base “Laisser-faire”. Dans le second cas (R0 égal à trois), une stratégie de dépistage systématique des porteurs symptomatiques et leur isolement (avec leur famille) est bien plus efficace pour casser la propagation de l’épidémie, même si les deux dispositifs de traçage commencent à produirent des effets importants pour un taux de couverture de l’ordre de 50% dans le scénario S3 et de 100% dans le scénario S4.

Ensuite, le scénario S4 “Traçage et isolement sélectif” présente un intérêt lorsque la dynamique épidémique est d’intensité moindre (R0 égal à deux), en raison à la fois de sa capacité à limiter le pic épidémique (sans pour autant faire mieux que le scénario d’isolement simple) mais également à cibler de manière précise la population à isoler, en épargnant notamment les personnes non contagieuses (saines et guéries). Ainsi, et dans le cas d’un R0 égal à deux seulement, le scénario S4 permettrait d’isoler presque deux fois moins de personnes (toutes contagieuses par ailleurs) que le scénario S2 et ceci même avec un taux de couverture faible (inférieur à 20%).

Nos simulations montrent enfin que l’efficacité du dispositif technologique de traçage modélisé - très proche dans ses principes de l’application StopCovid - ne semble pas résider en premier lieu dans sa capacité de traçage des contacts : au contraire, c’est bien le dépistage et l’isolement des porteurs symptomatiques qui reste le moteur principal de ce dispositif, le traçage précis des contacts venant compléter de manière secondaire ce premier tri. De ce point de vue, le taux de couverture de l’application améliore ses performances en terme de sélection des personnes à isoler, en évitant d’isoler de manière inutile des personnes non contagieuses, mais ne semble pas directement jouer de rôle dans sa capacité à maîtriser l’épidémie.

Ces résultats préliminaires suggèrent d’une part qu’une application de traçage du type StopCovid posséderait un domaine d’efficacité limité (R0 égal à deux) et d’autre part qu’elle devrait être associée de manière étroite avec des stratégies de dépistage et d’isolement très rigoureuses et efficaces. C’est à ce prix seulement qu’elle serait susceptible de présenter une éventuelle plus-value au regard d’une stratégie plus classique de dépistage et d’isolement des porteurs symptomatiques et de leur famille (stratégie par ailleurs très parcimonieuse et efficace en matière d’isolation de la population), essentiellement par sa capacité à n’isoler que des personnes contagieuses.

Reste à savoir si ce gain très relatif justifie le déploiement d’une telle application.

Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.

← Question précédente Question suivante →

Question 14 : Le traçage rétroactif des contacts par une application mobile peut-il faire la différence ?

L'application mobile StopCovid, destinée à briser la chaîne de transmission d'un malade en identifiant ses contacts rapprochés, fait couler beaucoup d’encre.