En l’état actuel de nos connaissances, il est difficile de donner une réponse simple et immédiate à cette question, par exemple : si une personne saine et une personne infectée entrent en contact, alors la personne saine possède n chances sur 100 de repartir avec son petit virus. Tout dépend en effet de la nature du contact, de sa durée, de la charge virale du porteur, etc.

Voici donc une question importante et d’apparence simple, à laquelle il est néanmoins difficile de répondre…et pourtant c’est exactement ce dont nous aurions besoin pour alimenter notre modèle de transmission du virus.
Ce que l’on sait en revanche, c’est que le R0 (ou nombre de reproduction de base) est élevé : sa valeur est estimée entre 2 et 3 par de nombreux spécialistes. Cela signifie qu’une personne infectée infectera en moyenne entre 2 et 3 autres personnes pendant la durée de l’épidémie.
Un groupe de chercheurs français a analysé les données du nombre de cas identifiés en France depuis le début de l’épidémie et a estimé que ce nombre de reproduction de base initial de l’épidémie de COVID-19 en France est proche de 2,5. Ils rappellent que, “à titre de comparaison, celui de la grippe saisonnière est généralement proche de 1,5. Cette forte valeur s’explique vraisemblablement par le fait que, contrairement à la grippe, il n’y a aucune immunité pré-existante dans la population”.
La manière de procéder est alors de chercher, pour la calibration du modèle (c’est à dire son rapprochement avec des valeurs empiriques) une valeur de probabilité de transmission inter-individuelle (comprise entre 0 et 1) qui soit cohérente avec cette valeur du R0 (comprise entre 2 et 3) estimée globalement.
Ce point précis fera vraisemblablement l’objet d’un post ultérieur, au même titre que la question de l’immunité d’ailleurs, mais ce qui nous intéresse plus précisément ici, c’est l’influence de cette valeur de probabilité de transmission sur la vitesse de propagation du virus dans une population constituée de personnes saines (vous vous rappelez peut-être que nous sommes en présence d’une maladie émergente contre laquelle personne, par définition, n’est immunisé).
Le meilleurs moyen de répondre à cette question est de reprendre notre modèle de base de la question 1 et de le faire tourner plusieurs fois, en fixant différentes valeurs à cette probabilité de transmission inter-individuelle.
On peut alors représenter les résultats obtenus sur un graphique, de manière à se forger une vision d’ensemble du processus.
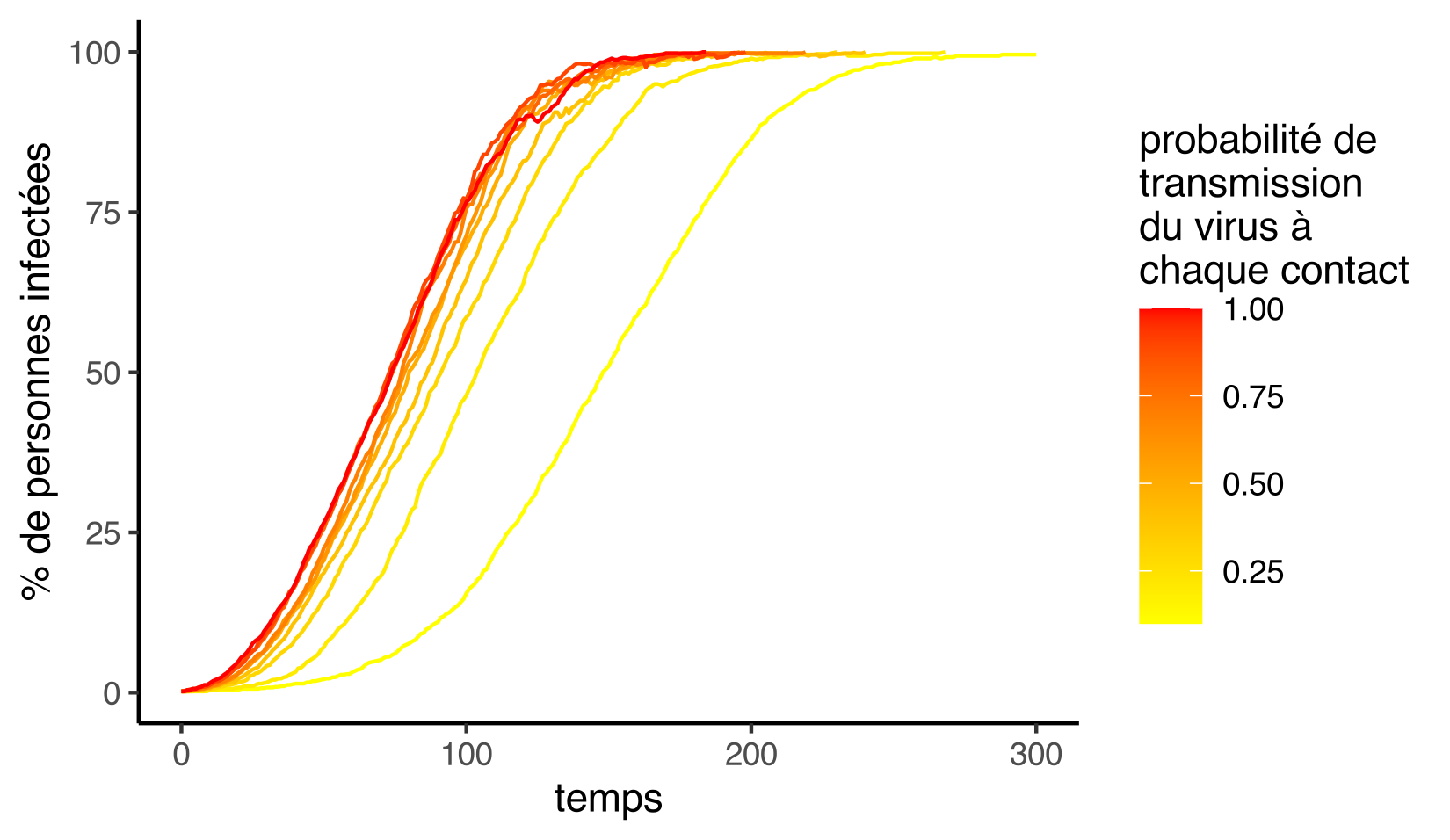
Ce graphique nous montre la progression de l’épidémie, depuis son début (une seule personne infectée) jusqu’à sa fin (tout le monde est infecté). Chaque courbe correspond à une simulation, avec une valeur de probabilité de transmission différente. En rouge, on trouve les courbes pour lesquelles cette valeur est proche de 1, en jaune celles pour lesquelles elle est proche de 0.
On constate que cette probabilité de transmission, que l’on peut voir comme un indicateur de la contagiosité du virus, a un impact direct sur la vitesse de propagation de celui-ci dans notre population d’individus sains et non immunisés. De manière logique, plus sa valeur est élevée (vagues rouges) et plus la vague épidémique sera précoce et rapide.
En revanche, seules des valeurs très faibles de cette probabilité de transmission permettent de réellement ralentir la progression de l’épidémie (la courbe jaune la plus à droite)…d’où l’importance des gestes barrières !
C’est aussi simple que ça.
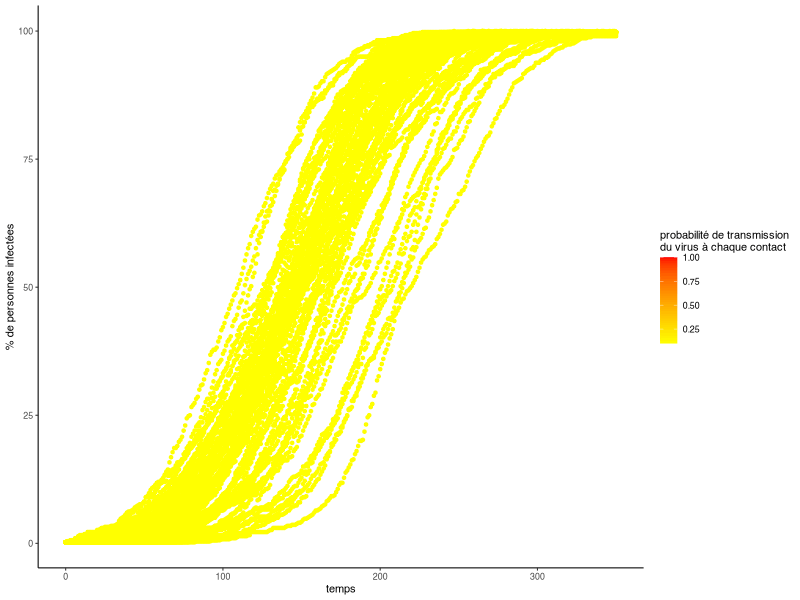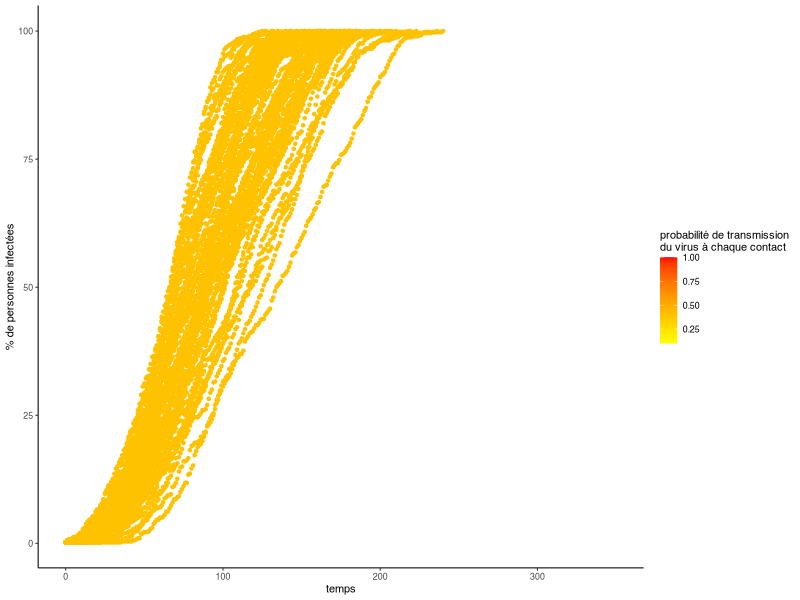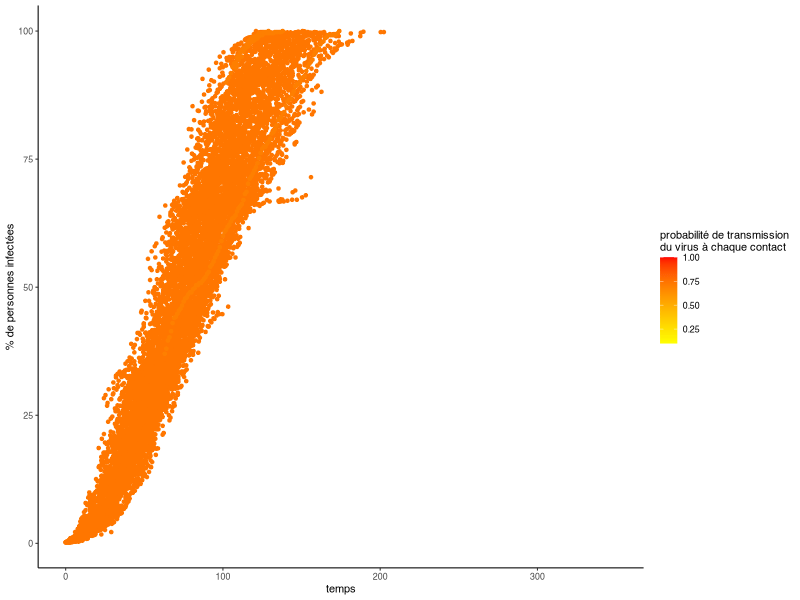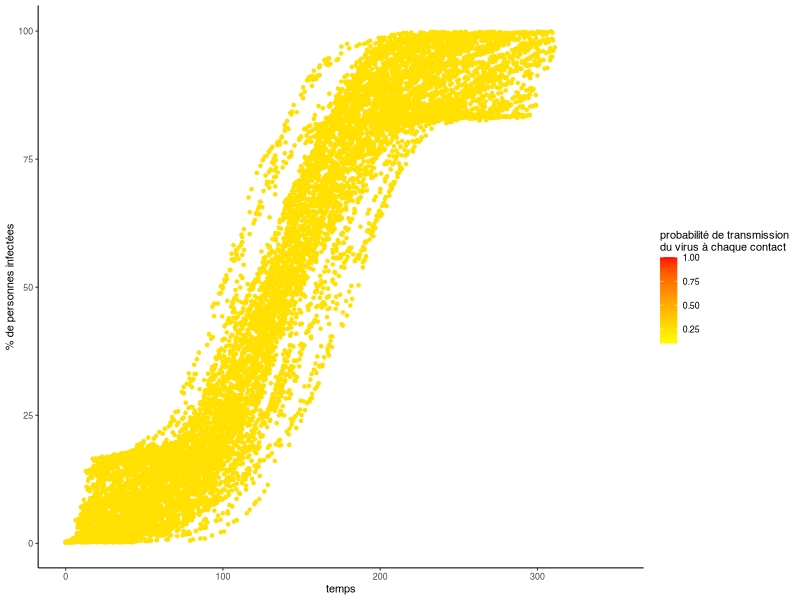
Représentation d’artiste (scientifique) de la vague épidémique pour différentes valeurs de transmissibilité du virus
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.