De nombreux phénomènes peuvent participer à l’infléchissement d’une courbe épidémique et il est par conséquent très important de pouvoir en faire de même dans les modèles. Concrètement, comment s’y prend-on ?
Nous allons répondre à cette question en mobilisant les outils théoriques et pratiques de l’épidémiologie mathématique. En toute simplicité bien sûr.
Prenons le cas d’école d’un modèle dans lequel les individus d’une population peuvent être soit sains (et donc susceptibles d’être infectés), soit infectés, soit guéris. On retrouve ici les composants de base de la plupart des modèles développés sur ce site. Dans le jargon de la modélisation des épidémies, on parle d’un modèle SIR (S pour Susceptible, I pour Infected et R pour Recovered). Ce type de modèle est très classique en épidémiologie mathématique.
Dans la plupart des questions précédentes sur ce site, nous nous sommes intéressés à un nombre réduit d’individus en interaction dont nous représentions les comportements individuels. Dans le cas où nous souhaitons modéliser des populations entières (à l’échelle de la France, de l’Europe, du Monde) il ne fait guère sens de vouloir représenter chaque comportement individuel, sauf si des raisons particulières motivent un tel investissement.
On raisonnera alors plutôt à partir de groupes de populations considérés comme homogènes par leurs caractéristiques et leurs comportements et on se limitera volontairement à un nombre réduit de paramètres : outre la population initiale dans chacun des états S, I et R, on retiendra essentiellement le taux de contact, le taux de contagion et le taux de guérison.
Bien entendu le taux de contagion, tout comme le taux de guérison, sont des paramètres propres à la maladie et aux mesures de prévention et de contrôle mises en place. Ils sont estimés à partir de données empiriques ou théoriques élaborées, depuis le début de l’épidémie, en différents endroits du globe.
Ce type de modèle, qui fait l’hypothèse (forte) que tout le monde va se comporter, contracter le virus et développer la maladie de la même manière, s’exprime essentiellement sous forme d’équations mathématiques. On peut toutefois, de manière très utile, le représenter également de manière graphique.
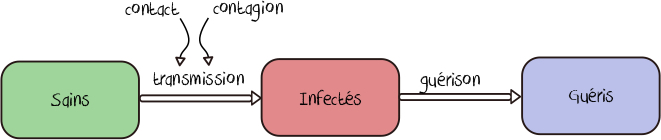
L’idée de base est en vérité toute simple (même si sa mise en oeuvre pratique l’est nettement moins) : à partir d’une situation de départ (par exemple ici 100 000 personnes saines et 1 personne infectée) on va calculer l’évolution du nombre de personnes saines, infectées et guéries à partir de leur nombre connu l’instant d’avant et de nos deux mécanismes de transmission et de guérison.
Une fois le modèle construit, sa résolution numérique produit les courbes épidémiques recherchées : on peut alors suivre l’évolution, au cours du temps, du nombre de personnes saines, infectées et guéries.
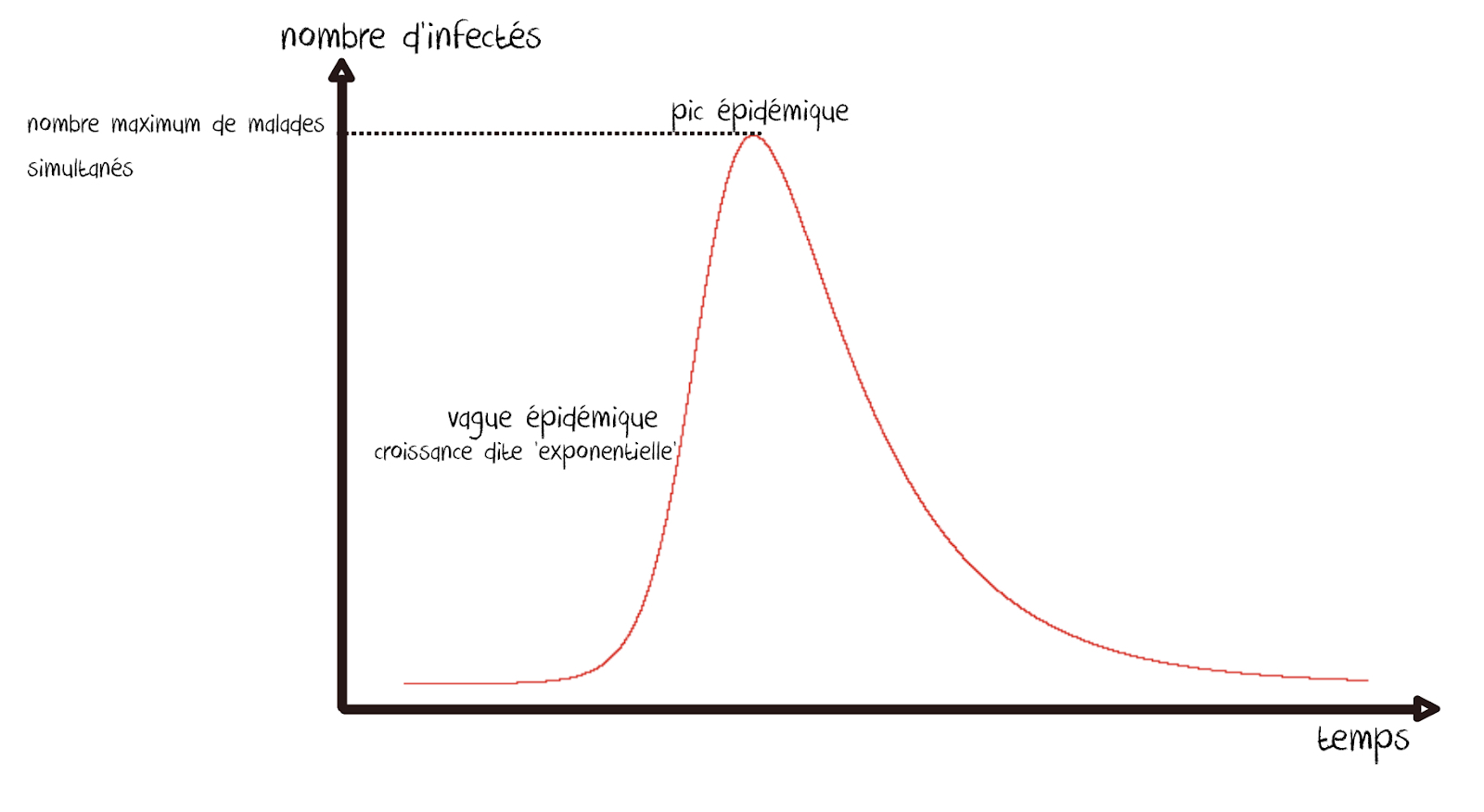
A partir de là et en fixant les mêmes conditions initiales (ici les nombres de personnes saines, infectées et guéries en début de simulation), on peut chercher à jouer sur chacun des paramètres (le taux de contact, le taux de contagion et le taux de guérison), de manière à étudier leurs effets sur la forme des courbes obtenues.
Un scénario de confinement nous poussera ainsi à définir un taux de contact inférieur à celui qui nous sert de référence, dans l’hypothèse d’un fonctionnement “normal”. De cette manière, la mise en place d’une période de confinement pendant notre épidémie virtuelle perturbera la courbe épidémique.
Si la fenêtre du simulateur est tronquée à l’affichage, il vous suffit d’effectuer un zoom arrière
Simuler l’impact du confinement sur la courbe épidémique
Vous vous demandez comment on a estimé le taux de contact avant et après confinement ? C’est par ici !
Tout ce que nous avons présenté ici peut sembler simple sur le papier. A un détail près : comment pouvons-nous estimer ce fameux taux de contact avant et pendant le confinement ?
Voilà une question incongrue n’est-ce pas ? En moyenne, combien d’interactions avec d’autres personnes avons-nous chaque jour ? Nous parlons bien sûr ici d’interactions entre des personnes impliquant une proximité physique suffisante pour rendre possible la transmission du virus. Il s’agit de ce qu’on appelle des contacts effectifs. On imagine tout de suite que cette valeur doit varier énormément entre un parisien qui prend le métro en heure de pointe et un habitant de Lozère qui vit retiré du monde. Et pourtant, il nous faut bien trouver un ordre de grandeur capable de caractériser notre population le plus largement possible (rappelez-vous, nous faisons l’hypothèse que les individus de notre population se comportent de manière identique).
Une étude réalisée en 2007 dans plusieurs pays européens nous apporte un éclairage intéressant. Cette étude portait sur 7290 participants sélectionnés au hasard et ayant rapporté au moyen de petits carnets de bord un total de 97 904 interactions proches au cours d’une même journée. Son principal résultat : le nombre moyen de contacts quotidiens impliquant une proximité physique importante y est estimé à 13,4 contacts par personne et par jour. Voici un ordre de grandeur intéressant à utiliser n’est-ce pas ?
Qu’en est-il maintenant en période de confinement ? S’il est bien suivi, les gens passent l’essentiel de leur temps chez eux et respectent la distanciation sociale lorsqu’ils sortent, donc la valeur devrait tendre vers zéro non ? Si vous avez lu la question 2 et la question 6, vous savez déjà que ce n’est pas si simple..
Nous n’avons pas trouvé dans la littérature de réponse précise à cette question, aussi fixons-nous ici une valeur par défaut de un seul contact par personne et par jour en moyenne pendant le confinement, soit 10 fois moins qu’en période normale.
Comment traduisons-nous maintenant ces deux valeurs (~10 et ~1 contacts) dans notre modèle ? Voyons cela en détail.
Nous savons déjà qu’à chaque instant de la simulation, une certaine quantité de personnes va quitter le stock des sains pour être dénombrée dans celui des infectés. Cette quantité dépend de quatre éléments :
- le nombre de personnes saines dans la population
- le nombre de personnes infectées dans la population
- le taux de contact
- le taux de contagion
Le nombre de contacts qu’une personne infectée va avoir à chaque instant avec une personne saine au cours de la simulation repose sur la multiplication de trois des termes : Sains x Infectés x Taux de contact
Si nous reprenons notre situation initiale (Sains = 100 000, Infectés = 1) alors, pour obtenir la valeur souhaitée de 10 contacts à chaque pas de temps entre une personne infectée et des personnes saines, il nous faut définir un taux de contact qui soit équivalent à 0.0001 dans la mesure où 100 000 x 1 x 0.0001 = 10
Bien entendu, cette valeur ne prend en compte que les interactions entre les personnes saines et les personnes infectées. Les interactions entre les personnes d’un même groupe (sains, infectés ou guéris) ou avec les personnes guéries ne sont donc pas prises en compte dans ce calcul.
Par ailleurs, notons que le nombre de personnes saines, tout comme le nombre de personnes infectées ou guéries, évolue au cours du temps. Le nombre d’interactions va donc tout naturellement évoluer au cours de l’épidémie. Cela se conçoit aisément car moins il y a de personnes saines, et moins il peut y avoir d’interactions entre des personnes infectées et des personnes saines (ce qui est d’ailleurs un des principes de l’immunité de groupe, comme vous le verrez dans la question 8 en cours de traitement).
Si vous avez lu attentivement ce que nous avons expliqué, une autre question doit se poser assez naturellement … vous l’avez ? …
Ce calcul est en effet actualisé à “chaque instant de la simulation”. Mais que représente le temps de la simulation dans notre cas ?
Cela pourra (peut-être ?) faire l’objet d’une prochaine réponse ;-)
En attendant, si vos souhaitez en savoir plus nous vous conseillons la lecture de ce rapport rédigé par l’une des meilleures équipes de recherche du domaine.
C’est aussi simple que ça.
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.