KOF KOF
Je ne sais pas si vous en avez entendu parler, mais nous subissons actuellement une pandémie de la maladie COVID-19 causée par le virus SARS-Cov-2. Au sein de l’épaisse couverture médiatique de ce bouleversement majeur de nos vies, une plus grande parole que d’habitude est laissée aux scientifiques, grâce à qui les plateaux télé et les journaux sont envahis de concepts pas évidents, comme les « modèles », les « simulations », des nombres appelés R0 (ou parfois juste R, est-ce le même ?), et un essaim d’autres notions auxquelles nous sommes habituellement rarement confrontés. Essayons d’y voir un peu plus clair. Cette saleté de SARS-Cov-2 s’installe à son aise dans nos alvéoles pulmonaires, et accessoirement notre muqueuse nasale. Quand nous soufflons, quand nous parlons, ou pire si nous toussons ou éternuons, nous émettons de petites gouttelettes de salive et de mucus, dont la taille varie grandement, de l’ordre du visible à l’œil nu au microscopique. Quand nous sommes infectés, ces gouttelettes transportent une charge de SARS-Cov-2 ; et si elles sont respirées par quelqu’un d’autre, éventuellement si elles atterrissent dans des yeux, ou même après un passage assez court sur une surface solide, elles peuvent provoquer une nouvelle infection. Les gouttelettes les plus fines peuvent même rester en suspension plusieurs heures, et se balader au gré des courants d’air. On comprend alors qu’il n’est pas possible de savoir précisément exactement qui, comment et à quelle seconde une contamination a eu lieu. Et pourtant… L’épidémiologie est la science qui s’attache à l’étude et l’analyse des conditions de santé et de maladie dans la population. Elle essaie donc, entre autres, de comprendre comment les épidémies naissent, apparaissent et meurent. Elle s’intéresse nécessairement aux contaminations. Un élément de sa panoplie est la construction d’une sorte particulière de compréhension scientifique d’un phénomène qu’on appelle un modèle.
Modéliser
Dans la première édition du dictionnaire de l’Académie française, en 1694, un “modelle” est un “Exemplaire, patron en relief, soit d’une statuë, soit de quelque autre ouvrage de Sculpture & d’Architecture, sur lequel on travaille ensuite pour faire l’ouvrage qu’on s’est proposé.” On retrouve là le sens de modèle réduit : une construction qui possèdera certaines caractéristiques de la chose modélisée (forme, proportions, couleur), mais pas d’autre (matériaux, dimensions). Cette simplification peut permettre à l’artiste ou l’artisan de mieux comprendre l’objet qu’il souhaite réaliser, d’explorer ses forces et ses faiblesses. Beaucoup de ces notions restent vraies pour les modèles scientifiques. Marvin Minsky, un des pères de l’intelligence artificielle, a proposé une définition de modèle scientifique qu’on pourrait traduire ainsi :
Pour un observateur O, A* est un modèle d’un objet A s’il permet à O de répondre à certaines questions qu’il a sur A.
A* sera une construction mentale, une simplification, d’un phénomène auquel on s’intéresse. Il pourra par ailleurs répondre à certaines questions et pas à d’autres. Il possède ainsi un domaine de validité, il fait certaines choses bien, d’autres non. Paul Valery disait : « Ce qui est simple est toujours faux. Ce qui ne l’est pas est inutilisable. » Et le modélisateur devra arbitrer ainsi entre ces extrémités… Mais revenons à notre paradoxe : comment peut-on dire des choses sur les épidémies alors qu’on ne peut pas prévoir si, dans des circonstances données, une personne donnée va en contaminer une autre ? C’est en fait comme les pièces de monnaies : si on en jette une en l’air, on aura bien du mal à prédire si elle atterrira sur pile ou sur face, mais si on en jette 10 000, on aura une bonne idée des proportions de pile et de face (c’est ce qu’on appelle parfois la « loi des grands nombres »). Les modèles épidémiologiques pourront dire des choses utiles sur des populations, mais pas grand-chose sur les individus. Vous vous souvenez ce qu’on disait sur les domaines de validité des modèles ? En voici un bon exemple.
SIR Mckendrick et Kermack
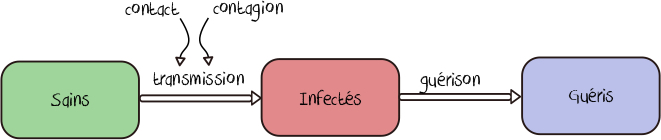
Les premiers modèles mathématiques en épidémiologie datent du début du XXème siècle, notamment avec les travaux des britanniques McKendrick et Kermack en 1927. Ces sont des modèles à compartiments. On a souvent dans ces modèles ce qu’on appelle des compartiments, qui sont des stocks de populations, Sains, Infectés et Retirés par exemple, c’est pourquoi on les appelle des modèles SIR. « Sain » désigne les personnes qui n’ont jamais eu la maladie considérée. « Infectés » désigne les personnes actuellement malades. « Retirés » désigne les personnes guéries, qu’on suppose désormais immunisées au moins temporairement à la maladie, et les personnes décédées. On a également des flux entre ces stocks, qui donc grossissent ou diminuent – si vous êtes un fidèle lecteur de CoVpréhension, vous reconnaîtrez des notions que nous employons dans de nombreuses questions, notamment la 10.
La mécanique de ces flux est gouvernée dans ces modèles par des équations différentielles, qui sont précisément des sortes d’équations qui relient la manière dont différentes valeurs évoluent (les équations qu’on voit au lycée, dites algébriques, relient plutôt directement les valeurs entre elles, par exemple surface = hauteur x largeur). Regardons-en juste une, pour voir à quoi ça ressemble :
N’ayez pas peur, c’est très simple. À gauche de l’équation, on a la variation au cours du temps du nombre de personnes dans le compartiment Sain. Si ce nombre est positif, on a de plus en plus de personnes saines, s’il est négatif il diminue. p est un paramètre de transmission, I le nombre d’infectés, S le nombre de sains. Plus on a d’infectés plus le nombre de sains diminue, plus on a de sains plus le nombre de sains diminue rapidement (les infectés ont plus de chance de croiser un sain). On a deux autres équations similaires, une pour l’évolution du nombre d’infectés I, une pour l’évolution du nombre de retirés R. Ces modèles sont les plus répandus : si, dans un reportage, on ne précise pas quel genre de modèle est utilisé, c’est sûrement un modèle de cette famille. Ce modèle est très bien expliqué dans la question 10. À partir de ces équations très simples, on va pouvoir essayer de comprendre la vitesse de propagation d’une maladie et la population touchée. Une notion importante est le nombre de personnes qu’une personne contaminée infectera au cours de sa contagion. On nommera ce nombre R0, le « nombre de reproduction de base ». Il a un sens un peu particulier dans le modèle SIR, parce qu’il y est supposé que la population est initialement entièrement Saine, que les Retirés sont à zéro, et qu’il n’y a initialement qu’un seul malade. Le nombre de reproductions évoluera au cours du temps, en fonction de l’évolution des compartiments ou de mesures sanitaires mises en place : on parlera alors de R(t). On considère souvent que ce R = ρ x c x d, où ρ est la probabilité de transmission à chaque contact, c le nombre de contact par unité de temps, et d la durée de la contagiosité. Mais que valent ces nombres ? Les modèles tels que SIR (et toutes les améliorations qu’ils ont connu depuis 1927) sont des modèles très agglomératifs, c’est-à-dire que de nombreuses caractéristiques des individus sont moyennées au sein de chaque compartiment de population. Pas facile de voir dans ces conditions comment les comportements individuels peuvent affecter l’épidémie : le port ou non du masque, la distanciation physique, ou même le respect du confinement. Comment affectent-ils notre « nombre de contacts par unité de temps » ? Heureusement, il existe une autre classe de modèles, que vous croisez souvent sur CoVpréhension avec des petits ronds de couleurs qui se baladent dans nos simulations, les modèles à base d’agents, ou Systèmes Multi-Agents (SMA).
Des agents pas très spéciaux
Dans un SMA on modélise chaque individu. Cela reste un modèle, donc l’individu est simplifié, on s’attache à isoler les caractéristiques qui nous semblent pertinentes pour répondre aux questions qu’on se pose : c’est pourquoi d’une question à l’autre on n’a pas exactement les mêmes agents dans CoVpréhension. Nos agents vont se déplacer, vivre leur vie dans leur espace simplifié, mais avec peut-être un domicile, un lieu de travail, des lieux de loisir. Et, en se croisant, se contaminer. Renonce-t-on alors au R(t) ? Un peu mais pas complètement. La durée de la contagiosité, on peut l’utiliser aussi bien que dans les modèles équationnels. Mais le nombre de contacts par unité de temps ne sera plus un nombre ou une fonction simple, il émergera des interactions de nos agents au cours de la simulation. On pourra alors essayer de se fixer un R0 ou un R(t) cible, et essayer d’agir sur la mobilité, ou la probabilité d’infection entre deux agents qui se rencontrent, et calibrer la simulation afin de faire se correspondre ces valeurs, qu’on évaluera « en moyenne » sur les simulations. Calibrer ? Simulations ? Mais Kezaco ?
Plonger un modèle dans le temps par la simulation.
Tous ces modèles, équationnels comme SMA, naissent nus : il faut trouver des données pour les habiller. Et c’est là aussi une étape très difficile et pleine de pièges. Quelle proportion de la population utilise un masque régulièrement ? Quelle proportion respecte le confinement ? Quelle est la probabilité d’infecter un de ses contacts ? Quelle proportion de la population a déjà été touchée par la maladie ? Ces données et bien d’autres encore, suivant les besoins du modèle et les question auxquelles on souhaiterait le voir répondre, seront utilisées de deux manières : en entrée, pour alimenter les paramètres du modèle ; et en sortie, pour le valider. Pour relier entrée et sortie, on utilisera parfois le calcul analytique et plus couramment un outil scientifique appelé simulation. Dans certains cas suffisamment simples, on peut calculer certaines valeurs de sorties de modèles équationnels juste en analysant le système d’équation. Dans un modèle SIR de base, on peut par exemple calculer directement le taux d’immunité collective, c’est-à-dire la proportion Rv de la population que doit atteindre la population du compartiment R des retirés à partir du R0 :
Mais c’est là l’exception plutôt que la règle : on ne peut généralement pas résoudre les systèmes d’équations des modèles. Résoudre, ce serait être capable de calculer toutes les valeurs des variables du modèle. Ce qu’on va pouvoir faire par contre, c’est les approximer par simulation. Une simulation informatique est l’exécution d’un programme qui fait varier certaines variables d’un modèle et calcule la valeur des autres en suivant les règles de ce modèle. Souvent, notamment dans les modèles d’épidémiologie qui nous préoccupent, c’est la variable « temps » qu’on va faire varier, par petits pas. Dans les modèles équationnels, on propagera ensuite ce petit pas de temps dans les autres variables. Par exemple, si on appelle dt notre petit pas de temps, et dS la petite variation de la population des Sains durant ce petit pas de temps, avec l’équation plus haut on pourra la calculer ainsi : dS=-p.I.S.dt Dans un SMA, un pas de temps pourra correspondre à une tranche de journée au cours de laquelle nos agents vaqueront aux occupations qui leur ont été programmées. Ainsi, on peut initialiser le modèle avec des données théoriques ou issues de mesures qu’on appelle des données d’entrée, dérouler son fonctionnement pas à pas, pour obtenir des valeurs de sorties pour des variables qu’on aura choisies en fonction des questions auxquelles on souhaitait que le modèle apporte une réponse (ex : hauteur du pic épidémique, proportion de la population touchée au cours de l’épidémie etc.). On parlera des valeurs prédites par le modèle. Et ensuite, nos modèles sont-ils enfin prêts à répondre aux questions qui ont motivé leur création ? Presque, mais il reste encore une étape : la calibration. En effet, les résultats d’un modèle peuvent dépendre d’un certain nombre de paramètres sur lesquels on n’a pas de données fiables. Vous vous souvenez quand on disait qu’il était difficile au niveau individuel de prédire si un individu dans des circonstances données en contaminera un autre ? Et pourtant, dans nos SMA, on a besoin d’une telle probabilité pour modéliser cette contamination : elle sera donc un paramètre de notre modèle. Calibrer un modèle, c’est calculer des valeurs pour ces paramètres. Pour cela, on utilisera la simulation pour calculer le problème inverse : sur un modèle calibré, on lui donne des valeurs d’entrées, il calcule les valeurs de sorties ; dans la calibration, on lui donne les valeurs d’entrées et certaines de sorties, et il doit calculer des valeurs pour les paramètres pour permettre cette connexion. C’est alors seulement qu’on utilisera ces modèles pour faire des prédictions, mais bien sûr sur d’autres valeurs que celles qu’on a utilisées pour la calibration. Par exemple, on peut calibrer un modèle SMA sur une épidémie entièrement « libre », pas du tout combattue, parce qu’on a des modèles validés sur un tel scénario ; et demander au modèle de prédire le pic épidémique ou la saturation des hôpitaux en rajoutant l’usage des masques ou de mesures de confinement, ou d’application d’aide au traçage de contacts.
Quel modèle pour quel usage ?
Nous avons vu précédemment des modèles équationnels et d’autres à base d’agents. Pourquoi utiliser les uns ou les autres ? Un des avantages des SMA, c’est qu’il est plus facile de dire par exemple « supposons que 70% des gens respectent la distanciation physique et 60% ont un masque, regardons comment cela affecte le processus d’infection ». Ils sont ainsi bien adaptés à l’exploration de scénarios de la forme « que se passerait-il si jamais… », bien en phase avec les objectifs de CoVpréhension. Un de leurs inconvénients en est par contre qu’en augmentant le niveau de détail, on ne bénéficie plus de la protection de la loi des grands nombres (comme avec nos 10 000 pièces). On peut prendre en compte plus de détails, mais il faut alors plus de données pour alimenter ces modèles, les calibrer, et vérifier si les caractéristiques qu’on a fixées pour nos agents, une fois moyennées et passées à la moulinette de milliers d’interactions avec les autres agents, nous permettent de retrouver, à l’échelle de la population, des valeurs qu’on peut mesurer dans le monde réel ou comparer à d’autres modèles établis. On pourra par exemple fixer que nos agents partent le matin de chez eux pour aller au travail, à pied ou en voiture, passeront le soir faire des courses avant de rentrer dormir, et calibrer qu’à l’échelle de la population ils ont bien 13,4 contacts par jour, pour prédire la vitesse de propagation de la maladie. De manière générale les modèles équationnels sont déterministes, ils ne font pas appel au hasard, on n’a besoin de ne les simuler qu’une fois pour des entrées données pour obtenir des sorties. Les SMA sont plus généralement stochastiques, ils font appel au hasard, pour savoir si tel ou tel individu va prendre sa voiture ou les transports en commun pour aller au travail, ou s’il est célibataire ou cohabite avec une famille nombreuse (tout en respectant à l’échelle de la population les proportions de types familiaux ou de moyens de transport). Par conséquent, pour utiliser un SMA, il faut répéter les simulations, pour obtenir des valeurs statistiquement significatives. En synthèse, les modèles équationnels raisonnent à l’échelle macroscopique, et sont efficaces pour interroger les grandes tendances, quand les SMA sont meilleurs à mesurer l’influence du micro sur le macro, du comportement individuel sur le collectif, quand on arrive à les calibrer correctement. Ce sont les grandes tendances, il existe des approches hybrides qui nuancent ce qui vient d’être dit.
Prédire et décider
Nous comprenons à présent peut-être mieux que les modèles sont des outils scientifiques construits pour répondre à des questions précises. Il en existe de différentes sortes, les deux grandes familles étant les modèles équationnels et les Systèmes Multi-Agents. On les calibre et les interroge par des simulations informatiques. Ils peuvent alors, pour des données d’entrée, prédire des données de sortie. Ces résultats scientifiques sont ensuite partagés par leurs créateurs avec leurs pairs au sein d’articles dans des conférences et revues scientifiques spécialisées. Modèles et expérimentations sont alors critiqués constructivement par les relecteurs, ce qui peut amener à de nouvelles expérimentations avant que l’article soit finalement accepté. Cette publication scientifique pourra alors elle-même être vulgarisée par la presse généraliste, idéalement par l’intermédiaire d’un journaliste spécialisé, et nous sommes ainsi revenus au début de ce post.
Rappel : les modèles développés sur ce site sont des modèles pédagogiques, bien plus simples que les modèles construits et mis en oeuvre par d’autres équipes scientifiques travaillant sur la COVID-19. Ils ne se substituent pas à ces modèles de référence et ne peuvent pas être utilisés à leur place pour mener des expertises, diagnostics ou pronostics. Notre objectif est de contribuer à la création, au sein de la population, d’une meilleure connaissance des moteurs de cette épidémie qui nous concerne toutes et tous.