Since transmission between individuals is the main vector of the epidemic, let’s see what happens when people can no longer meet each other!
This logic seems sensible doesn’t it? If everyone is confined, those who have the disease won’t be able to spread it as they will now also be in isolation if they were carrying the virus when lockdown started. If we wait long enough that carriers stop being contagious, the problem should be resolvable without major difficulties.
Can it really be that simple though?
Here is a game which helps us illustrate this question. You can play with it below, but let’s agree on the rules first.
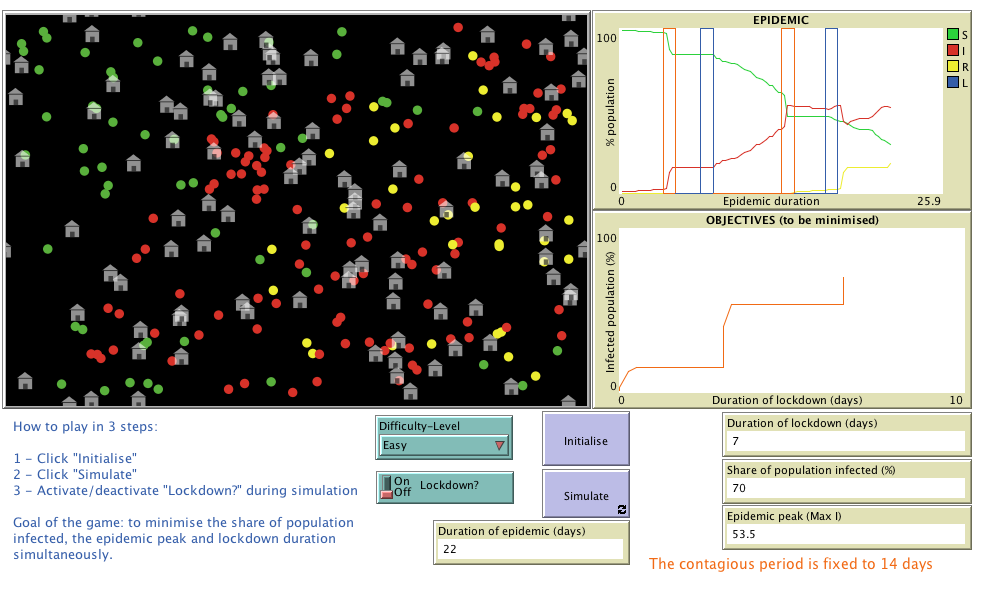
When you click “Initialise”, you get a population composed of healthy individuals (the green dots) and of infected individuals (the red dots). Each individual in the simulation owns a house to lock themselves down. We recognise that this is a distorted vision of reality, but a future post will explore the inequalities of being in lockdown.
A house can be shared by several individuals who will all be infected if one of them has the virus. After 14 days, infected individuals are considered cured (the grey dots). They are no longer contagious and can’t be infected again.
When you click “Simulate”, individuals move around at random and the virus spreads during people’s interactions.
By switching up or down “Lockdown?”, you will activate or deactivate the lockdown.
During lockdown, each individual will stay home and their epidemic state will evolve as follows:
- Healthy people will stay healthy if they are alone in the house or with other healthy people;
- Infected people will be cured when their infection is more than 14 days old;
- Healthy people who share a house with one or several infected people will become infected.
If you agree with these rules, you are ready to play. The goal, for each scenario, is to reach the end of the epidemic (where no one is infected anymore) with the least amount of days spent in lockdown, the least amount of people infected over the whole duration of the epidemic, and the smallest possible epidemic peak. These three indicators are shown on the lower right corner of the screen and are updated throughout the simulation: “number of days in lockdown”, “share of population infected (%)” and “epidemic peak (Max I)”.
There are two graphs to help guide you.
The one at the top (“Evolution of the epidemic”) gives an indication of the global state of your population over time, which starts by convention when you click “Simulate”.
You will find curves on this graph that you may be familiar with already if you have read the previous posts. The green curve shows the proportion of healthy people in the population. The red curve shows the proportion of infected people and its maximum value corresponds to the epidemic peak, expressed as a percentage of total population. Finally, the grey curve shows the proportion of cured people. At any time t, the sum of the three amounts to 100%. The start date (in blue) and end date (in purple) of lockdown are also shown on the graph every time you click “Lockdown?”.
The bottom graph (“Goals reached”) shows you how you score on two of your goals: the “number of days in lockdown” and the “share of population infected (%)”. The third goal “epidemic peak (Max I)” can be tracked on the top graph.
Here you go, it’s your turn to try and contain this epidemic. Remember, you have to win on all three fronts: to have the least people infected by the virus, to flatten the curve of the epidemic peak AND to minimize the lockdown duration.
If the simulator window is truncated, try to zoom out
So, do you still think that the question of lockdown is a simple one?
You may have noticed that the driving force of the epidemic is powerful, which makes it harder to stop and easier to relapse if the lockdown is lifted too early.
Have you tried to win on all fronts, by minimizing the three goals, or have you decided that some goals are less important than others? Have you decided that flattening the curve to avoid a saturation of the healthcare system is more important than the spread of the virus in the population? Or maybe that the lockdown duration should be the key variable to minimize in order to reduce the stress on the economy? These are the kinds of choices each society has to make when implementing a lockdown.
By the way, have you identified the three key hypotheses that this game needs to function?
First, the game assumes that people can stay home without going out at all for more than 15 days if necessary. The simulated individuals do not try to contest or breach the lockdown.
Second, our simulated community lives in autarky, with no one arriving from the outside once the lockdown is over, suggesting to our healthy population that it is protected against a relapse of the epidemic.
Last, but not least, our virtual population is ridiculously small, 200 people maximum.
None of these hypotheses is viable!
In reality, people have to go out during lockdown, even if going out is restricted by the authorities. Everyone has to at least feed themselves and not everyone can work from home. During each trip outside, exposure to the virus is lower than usual, but it is not null, which creates an epidemic dynamic which is weak yet constant. In a bigger population than the one represented in the game, this background dynamic will mechanically increase the duration of lockdown because new cases will emerge regularly.
Besides, ending the lockdown is a really tricky question because
Finally, lifting the lockdown is really a tricky question. Two main points jump out. First, if the lockdown is lifted too early, the epidemic will relapse even stronger. You may have notice this dynamics in the simulator. Second, even if we manage to contain the epidemic with a long and efficient lockdown, new arrivals of people carrying the virus from further afield will cause the epidemic to relapse in the population since a large share of people are not yet immune to it, having been protected from the virus by the lockdown.
It is as simple as that.
A model with more details and able to explore alternative lockdown scenarios is in the making. Stay tuned!
Reminder: the models developed on this website are for educational purposes only. They are a lot simpler than models built and deployed by other teams working on COVID-19. They are not substitutes for these reference models and cannot be used to make diagnoses or forecasts. Our goal instead is to raise awareness about this epidemic and its drivers. Going further